Difference between revisions of "Liouville function"
(Importing text file) |
|||
| Line 20: | Line 20: | ||
The Liouville function was introduced by J. Liouville. | The Liouville function was introduced by J. Liouville. | ||
| + | |||
| + | Liouville function satisfies the explicit formula $$ \sum_{n=1}^\infty \frac{\lambda(n)}{\sqrt{n}}g(\log n) = \sum_{\rho}\frac{h( \gamma)\zeta(2 \rho )}{\zeta'( \rho)} + \frac{1}{\zeta (1/2)}\int_{-\infty}^\infty dx \, g(x) $$ | ||
| + | |||
| + | where $ g(u)= \frac{1}{2\pi} \int_{-\infty}^\infty h(x)\exp(-iux) $ form a Fourier transform pair | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K. Chandrasekharan, "Arithmetical functions" , Springer (1970)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> K. Chandrasekharan, "Arithmetical functions" , Springer (1970)</TD></TR></table> | ||
Latest revision as of 11:53, 17 January 2020
The arithmetic function  defined by
defined by
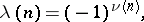 |
where  is the number of prime factors of
is the number of prime factors of  . The Liouville function is closely connected with the Möbius function
. The Liouville function is closely connected with the Möbius function 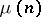 :
:
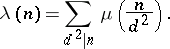 |
In number theory an important estimate is that of the sum
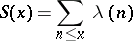 |
as  . There is a conjecture that
. There is a conjecture that
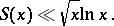 |
The most recent result, obtained by a method of I.M. Vinogradov, has the form
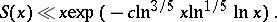 |
The Liouville function was introduced by J. Liouville.
Liouville function satisfies the explicit formula $$ \sum_{n=1}^\infty \frac{\lambda(n)}{\sqrt{n}}g(\log n) = \sum_{\rho}\frac{h( \gamma)\zeta(2 \rho )}{\zeta'( \rho)} + \frac{1}{\zeta (1/2)}\int_{-\infty}^\infty dx \, g(x) $$
where $ g(u)= \frac{1}{2\pi} \int_{-\infty}^\infty h(x)\exp(-iux) $ form a Fourier transform pair
References
| [1] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [2] | K. Chandrasekharan, "Arithmetical functions" , Springer (1970) |
Liouville function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Liouville_function&oldid=17862