Difference between revisions of "Lie triple system"
m (link) |
m (Added that the standard embedding is Z2-graded) |
||
| Line 13: | Line 13: | ||
Setting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004011.png" />, then (a3) means that the left endomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004012.png" /> is a derivation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004013.png" /> (cf. also [[Derivation in a ring|Derivation in a ring]]). Thus one denotes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004014.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004015.png" />. | Setting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004011.png" />, then (a3) means that the left endomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004012.png" /> is a derivation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004013.png" /> (cf. also [[Derivation in a ring|Derivation in a ring]]). Thus one denotes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004014.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004015.png" />. | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004016.png" /> be a Lie triple system and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004017.png" /> be the vector space of the direct sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004019.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004020.png" /> is a [[Lie algebra|Lie algebra]] with respect to the product | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004016.png" /> be a Lie triple system and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004017.png" /> be the vector space of the direct sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004019.png" />. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004020.png" /> is a Z2-graded [[Lie algebra|Lie algebra]] with respect to the product |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l130/l130040/l13004021.png" /></td> </tr></table> | ||
Revision as of 11:35, 30 April 2018
A triple system is a vector space  over a field
over a field  together with a
together with a  -trilinear mapping
-trilinear mapping 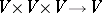 .
.
A vector space  with triple product
with triple product  is said to be a Lie triple system if
is said to be a Lie triple system if
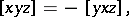 | (a1) |
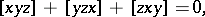 | (a2) |
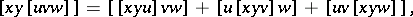 | (a3) |
for all  .
.
Setting 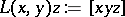 , then (a3) means that the left endomorphism
, then (a3) means that the left endomorphism 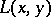 is a derivation of
is a derivation of 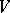 (cf. also Derivation in a ring). Thus one denotes
(cf. also Derivation in a ring). Thus one denotes 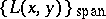 by
by 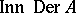 .
.
Let 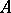 be a Lie triple system and let
be a Lie triple system and let 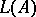 be the vector space of the direct sum of
be the vector space of the direct sum of 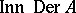 and
and  . Then
. Then 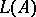 is a Z2-graded Lie algebra with respect to the product
is a Z2-graded Lie algebra with respect to the product
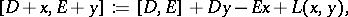 |
where 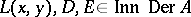 ,
,  .
.
This algebra is called the standard embedding Lie algebra associated with the Lie triple system 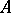 . This implies that
. This implies that 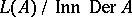 is a homogeneous symmetric space (cf. also Homogeneous space; Symmetric space), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [a4], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [a1]. A general consideration of supertriple systems is given in [a2] and [a5].
is a homogeneous symmetric space (cf. also Homogeneous space; Symmetric space), that is, it is important in the correspondence with geometric phenomena and algebraic systems. The relationship between Riemannian globally symmetric spaces and Lie triple systems is given in [a4], and the relationship between totally geodesic submanifolds and Lie triple systems is given in [a1]. A general consideration of supertriple systems is given in [a2] and [a5].
Note that this kind of triple system is completely different from the combinatorial one of, e.g., a Steiner triple system.
References
| [a1] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) |
| [a2] | N. Kamiya, S. Okubo, "On 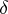 -Lie supertriple systems associated with -Lie supertriple systems associated with 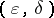 -Freudenthal–Kantor supertriple systems" Proc. Edinburgh Math. Soc. , 43 (2000) pp. 243–260 -Freudenthal–Kantor supertriple systems" Proc. Edinburgh Math. Soc. , 43 (2000) pp. 243–260 |
| [a3] | W.G. Lister, "A structure theory of Lie triple systems" Trans. Amer. Math. Soc. , 72 (1952) pp. 217–242 |
| [a4] | O. Loos, "Symmetric spaces" , Benjamin (1969) |
| [a5] | S. Okubo, N. Kamiya, "Jordan–Lie super algebra and Jordan–Lie triple system" J. Algebra , 198 : 2 (1997) pp. 388–411 |
Lie triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_triple_system&oldid=42982