Bishop-Phelps theorem

Consider a real Banach space , its (closed convex) unit ball , and its adjoint space of continuous linear functionals (cf. Linear functional). If , its norm is defined as its supremum on the closed convex set , that is, . The fundamental Hahn–Banach theorem implies that if 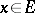and , then there exists a continuous linear functional such that 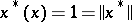. Thus, these "Hahn–Banach functionals" attain their suprema on , and by taking all positive scalar multiples of such functions, there are clearly "many" of them. The Bishop–Phelps theorem [a1] asserts that such norm-attaining functionals are actually norm dense in 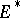. (James' theorem [a4] shows that if every element of 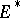attains its supremum on 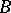, then 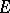is necessarily reflexive, cf. Reflexive space.) A more general Bishop–Phelps theorem yields the same norm density conclusion for the set of functionals in 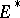which attain their supremum on an arbitrary non-empty closed convex bounded subset 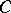of 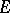(the support functionals of 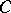). In fact, if 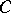is any non-empty closed convex subset of 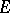, its support functionals are norm dense among those functionals which are bounded above on 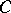; moreover, the points of 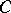at which support functionals attain their supremum on 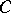(the support points) are dense in the boundary of 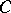. (This contrasts with a geometric version of the Hahn–Banach theorem, which guarantees that every boundary point of a closed convex set 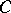is a support point, provided 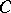has non-empty interior.)

This last result leads to the Brøndsted–Rockafellar theorem [a2], fundamental in convex analysis, about extended-real-valued lower semi-continuous convex functions 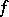on 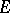which are proper, in the sense that 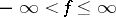and 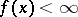for at least one point . The epigraph 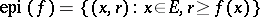of such a function is a non-empty closed convex subset of the product space 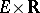( 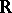the real numbers) and the subgradients of define support functionals of 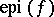. The set of all subgradients to 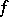at (where 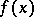is finite) form the subdifferential

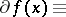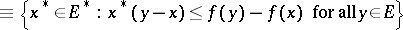of 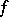at . The Brøndsted–Rockafellar theorem [a2] yields density, within the set of points where 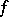is finite, of those for which is non-empty.

See also [a3] for the Bishop–Phelps and James theorems, [a5] for the Bishop–Phelps and Brøndsted–Rockafellar theorems.

References

[a1]	E. Bishop, R.R. Phelps, "The support functionals of a convex set" P. Klee (ed.) , Convexity , Proc. Symp. Pure Math. , 7 , Amer. Math. Soc. (1963) pp. 27–35 Zbl 0149.08601
[a2]	A. Brøndsted, R.T. Rockafellar, "On the subdifferentiability of convex functions" Proc. Amer. Math. Soc. , 16 (1965) pp. 605–611
[a3]	J. Diestel, "Geometry of Banach spaces: Selected topics" , Lecture Notes in Mathematics , 485 , Springer (1975)
[a4]	R.C. James, "Reflexivity and the supremum of linear functionals" Israel J. Math. , 13 (1972) pp. 289–300
[a5]	R.R. Phelps, "Convex functions, monotone operators and differentiability" , Lecture Notes in Mathematics , 1364 , Springer (1993) (Edition: Second)
[b1]	Andrzej Granas, James Dugundji, "Fixed Point Theory", Springer Monographs in Mathematics, Springer (2003) ISBN 0-387-00173-5 Zbl 1025.47002