Difference between revisions of "Proximal point methods in mathematical programming"
(Importing text file) |
m (link) |
||
| Line 7: | Line 7: | ||
i) The sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102507.png" /> is well defined (in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102508.png" /> has a unique zero), converges to a zero of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102509.png" /> if such a zero exists, and is unbounded otherwise. | i) The sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102507.png" /> is well defined (in the sense that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102508.png" /> has a unique zero), converges to a zero of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p1102509.png" /> if such a zero exists, and is unbounded otherwise. | ||
| − | ii) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025010.png" /> is strongly monotone, then the convergence rate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025011.png" /> is linear, and super-linear when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025012.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025013.png" /> is the [[Subdifferential|subdifferential]] of a convex polyhedral function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025014.png" /> (i.e. the epigraph of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025015.png" /> is a polyhedron), then convergence is finite. | + | ii) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025010.png" /> is strongly monotone, then the convergence rate of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025011.png" /> is linear, and super-linear when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025012.png" />. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025013.png" /> is the [[Subdifferential|subdifferential]] of a convex polyhedral function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025014.png" /> (i.e. the [[epigraph]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025015.png" /> is a polyhedron), then convergence is finite. |
iii) Convergence properties are preserved under inexact computation of the zero of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025016.png" />, in the following sense: (a1) is replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025017.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025019.png" />. | iii) Convergence properties are preserved under inexact computation of the zero of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025016.png" />, in the following sense: (a1) is replaced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025017.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110250/p11025019.png" />. | ||
Revision as of 17:01, 7 May 2017
The proximal point method for finding a zero of a maximal monotone operator  generates a sequence
generates a sequence  , starting with any
, starting with any 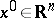 , whose iteration formula is given by
, whose iteration formula is given by
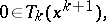 | (a1) |
where 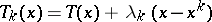 and
and 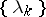 is a bounded sequence of positive real numbers. The origin of the method can be traced back to the study of regularization of ill-posed problems (see [a3]; Regularization method; Ill-posed problems) and is closely related to Moreau–Yoshida convolution (see [a5]). A survey on the method can be found in [a4]. The basic properties of the method, as established in [a7], are as follows.
is a bounded sequence of positive real numbers. The origin of the method can be traced back to the study of regularization of ill-posed problems (see [a3]; Regularization method; Ill-posed problems) and is closely related to Moreau–Yoshida convolution (see [a5]). A survey on the method can be found in [a4]. The basic properties of the method, as established in [a7], are as follows.
i) The sequence 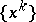 is well defined (in the sense that
is well defined (in the sense that 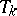 has a unique zero), converges to a zero of
has a unique zero), converges to a zero of 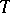 if such a zero exists, and is unbounded otherwise.
if such a zero exists, and is unbounded otherwise.
ii) If 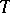 is strongly monotone, then the convergence rate of
is strongly monotone, then the convergence rate of 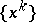 is linear, and super-linear when
is linear, and super-linear when 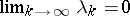 . When
. When 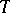 is the subdifferential of a convex polyhedral function
is the subdifferential of a convex polyhedral function 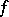 (i.e. the epigraph of
(i.e. the epigraph of 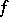 is a polyhedron), then convergence is finite.
is a polyhedron), then convergence is finite.
iii) Convergence properties are preserved under inexact computation of the zero of 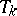 , in the following sense: (a1) is replaced by
, in the following sense: (a1) is replaced by 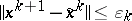 , where
, where 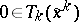 and
and 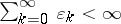 .
.
When 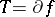 (the subdifferential of a convex function
(the subdifferential of a convex function 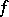 ), then (a1) is equivalent to
), then (a1) is equivalent to
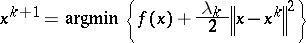 | (a2) |
and the zeros of 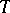 are the minimizers of
are the minimizers of 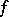 , so that
, so that 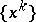 converges to a minimizer of
converges to a minimizer of 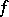 . If
. If 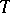 is the subdifferential of the dual objective of a convex optimization problem, then the sequence
is the subdifferential of the dual objective of a convex optimization problem, then the sequence 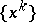 coincides with the dual sequence generated by the augmented Lagrangian method (see [a6]).
coincides with the dual sequence generated by the augmented Lagrangian method (see [a6]).
All these properties hold also for maximal monotone operators in a Hilbert space, in which case convergence is understood in the sense of the weak topology.
The proximal point method can be applied to problems with convex constraints, e.g. the variational inequality problem 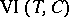 , for a closed and convex set
, for a closed and convex set 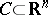 , which consists of finding a
, which consists of finding a 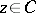 such that there exists an
such that there exists an 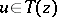 satisfying
satisfying 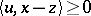 for all
for all 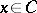 . When
. When 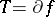 with convex
with convex 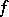 ,
, 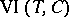 reduces to minimizing
reduces to minimizing 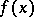 subject to
subject to 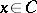 . For applying the proximal point method to
. For applying the proximal point method to 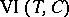 it suffices to replace
it suffices to replace 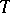 by
by 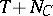 , where
, where 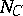 is the normal cone operator of
is the normal cone operator of 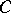 . In such a case, (a1) becomes equivalent to stating that
. In such a case, (a1) becomes equivalent to stating that 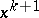 solves
solves 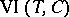 and (a2) becomes
and (a2) becomes
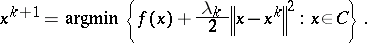 |
There is another way to deal with constrained problems in the context of the proximal point method, without introducing the normal cone of 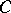 , for the case when
, for the case when 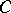 has non-empty interior and when a boundary-coercive Bregman function
has non-empty interior and when a boundary-coercive Bregman function 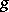 with zone
with zone 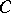 is available. In this case the method starts with
is available. In this case the method starts with 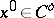 (the interior of
(the interior of 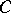 ) and the iterative formula is still (a1) but now
) and the iterative formula is still (a1) but now 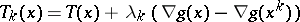 . In the optimization case, i.e.
. In the optimization case, i.e. 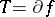 , this formula is equivalent to
, this formula is equivalent to
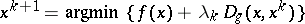 |
where 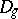 is the Bregman distance associated with
is the Bregman distance associated with 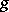 . This generalization of the proximal point method is an interior point algorithm, in the sense that the sequence
. This generalization of the proximal point method is an interior point algorithm, in the sense that the sequence 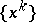 lies in the interior of
lies in the interior of 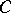 (cf. also Interior-point methods in mathematical programming). Under certain technical hypotheses on
(cf. also Interior-point methods in mathematical programming). Under certain technical hypotheses on 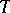 , satisfied, e.g., when
, satisfied, e.g., when 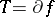 , property i) above still holds, i.e. the sequence
, property i) above still holds, i.e. the sequence 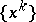 converges to a solution of
converges to a solution of 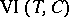 when a solution exists and is unbounded otherwise, [a8]. A property of this generalization, not shared by the original proximal point method (a1), is that for certain problems, including linear programming and quadratic programming, the limit of the sequence
when a solution exists and is unbounded otherwise, [a8]. A property of this generalization, not shared by the original proximal point method (a1), is that for certain problems, including linear programming and quadratic programming, the limit of the sequence 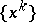 is the solution of the problem which minimizes the Bregman distance to the initial iterate
is the solution of the problem which minimizes the Bregman distance to the initial iterate 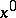 (see [a2], [a10]). This procedure also generates augmented Lagrangian-type methods when
(see [a2], [a10]). This procedure also generates augmented Lagrangian-type methods when 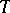 is the subdifferential of the dual objective of a convex optimization problem. For instance, when
is the subdifferential of the dual objective of a convex optimization problem. For instance, when 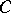 is the non-negative orthant of
is the non-negative orthant of 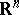 and
and 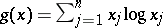 , the sequence
, the sequence 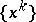 coincides with the dual sequence of the Bertsekas exponential multipliers method (see [a1], [a11]).
coincides with the dual sequence of the Bertsekas exponential multipliers method (see [a1], [a11]).
Finally, some results are available for the proximal point method with Bregman distances under inexact solutions of the subproblems, in the spirit of property iii) above, [a9]. Convergence is guaranteed for the sequence generated by 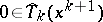 , with
, with 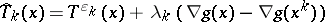 , where
, where 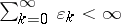 and, for any monotone operator
and, for any monotone operator 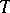 and any
and any 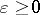 ,
, 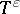 is defined as
is defined as
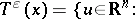 |
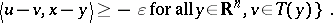 |
References
| [a1] | D. Bertsekas, "Constrained optimization and Lagrange multipliers" , Acad. Press (1982) |
| [a2] | A.N. Iusem, "On some properties of generalized proximal point methods for quadratic and linear programming" J. Optimization Th. Appl. , 85 (1995) pp. 593–612 |
| [a3] | M.A. Krasnoselskii, "Two observations about the method of successive approximations" Uspekhi Mat. Nauk , 10 (1955) pp. 123–127 (In Russian) |
| [a4] | B. Lemaire, "The proximal algorithm" J.P. Penot (ed.) , Internat. Ser. Numer. Math. , 87 , Birkhäuser (1989) pp. 73–87 |
| [a5] | J. Moreau, "Proximité et dualité dans un espace hilbertien" Bull. Soc. Math. France , 93 (1965) pp. 273–299 |
| [a6] | R.T. Rockafellar, "Augmented Lagrangians and applications of the proximal point algorithm in convex programming" Math. of Oper. Res. , 1 (1976) pp. 97–116 |
| [a7] | R.T. Rockafellar, "Monotone operators and the proximal point algorithm" SIAM J. Control Optim. , 14 (1976) pp. 877–898 |
| [a8] | R.S. Burachik, A.N. Iusem, "A generalized proximal point algorithm for the variational inequality in a Hilbert space" SIAM J. Optim. (to appear) |
| [a9] | R.S. Burachik, A.N. Iusem, B.F. Svaiter, "Enlargement of monotone operators with applications to variational inequalities" Set Valued Anal. (to appear) |
| [a10] | A.N. Iusem, "On some properties of generalized proximal point methods for variational inequalities" J. Optim. Th. & Appl. (to appear) |
| [a11] | A.N. Iusem, B.F. Svaiter, M. Teboulle, "Entropy-like proximal methods in convex programming" Math. of Oper. Res. , 19 (1994) pp. 790–814 |
Proximal point methods in mathematical programming. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Proximal_point_methods_in_mathematical_programming&oldid=14222