Difference between revisions of "Derangement"
(Importing text file) |
m (Richard Pinch moved page Inversion (in combinatorics) to Derangement: Better translation, see talk page) |
(No difference)
| |
Revision as of 07:18, 2 December 2016
derangement
A permutation of 
elements in which the element 
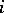cannot occupy the 
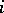-th position, 
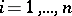. The problem of calculating the number 
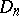of derangements is known as the "problème des rencontresproblème des rencontres" . The following formula holds:
 |
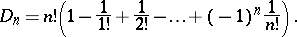Derangements are a special case of permutations satisfying a specific restriction on the position of the permuted elements. For example, the "problème des ménagesproblème des ménages" consists in calculating the number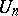 
of permutations conflicting with the two permutations 
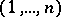and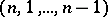 
. (Two permutations of 
elements are called conflicting if the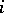 
-th element occupies different positions in each of them for all 
). The number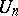 
is given by the formula:
 |
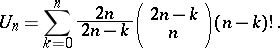The number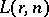 
of Latin squares (cf. Latin square) of size 
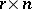for 
can be calculated in terms of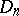 
and 
by the formulas
 |
 |
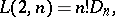References
| [1] | H.J. Ryser, "Combinatorial mathematics" , Carus Math. Monogr. , 14 , Wiley & Math. Assoc. Amer. (1963) |
| [2] | J. Riordan, "An introduction to combinatorial mathematics" , Wiley (1958) |
Derangement. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Derangement&oldid=18965