Difference between revisions of "Natural sequence"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
''natural number sequence'' | ''natural number sequence'' | ||
| − | The non-empty set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661101.png" /> in which a unary operation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661102.png" /> is defined (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661103.png" /> is a single-valued mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661104.png" /> into itself) satisfying the following conditions (the [[Peano axioms|Peano axioms]]): | + | The non-empty set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661101.png" /> in which a [[unary operation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661102.png" /> is defined (i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661103.png" /> is a single-valued mapping of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661104.png" /> into itself) satisfying the following conditions (the [[Peano axioms|Peano axioms]]): |
1) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661105.png" />, | 1) for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066110/n0661105.png" />, | ||
Revision as of 19:14, 13 November 2016
natural number sequence
The non-empty set 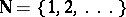 in which a unary operation
in which a unary operation 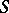 is defined (i.e.
is defined (i.e.  is a single-valued mapping of
is a single-valued mapping of 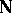 into itself) satisfying the following conditions (the Peano axioms):
into itself) satisfying the following conditions (the Peano axioms):
1) for any 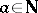 ,
,
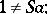 |
2) for any 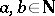 : If
: If
 |
then
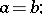 |
3) any subset of  that contains 1 and that together with any element
that contains 1 and that together with any element  also contains
also contains 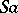 , is necessarily the whole of
, is necessarily the whole of 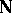 (axiom of induction).
(axiom of induction).
The element 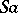 is usually called the immediate successor of
is usually called the immediate successor of  . The natural sequence is a totally ordered set. It can be proved that the conditions
. The natural sequence is a totally ordered set. It can be proved that the conditions
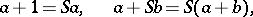 |
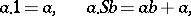 |
where  and
and 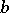 are arbitrary elements of
are arbitrary elements of  , define binary operations
, define binary operations  and
and  on
on 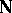 . The system
. The system 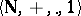 is the system of natural numbers (cf. Natural number).
is the system of natural numbers (cf. Natural number).
References
| [1] | B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German) |
Comments
Often, the natural number sequence is started at  , cf. also Natural number.
, cf. also Natural number.
The system 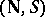 is the only (up to an isomorphism) system satisfying the Peano axioms.
is the only (up to an isomorphism) system satisfying the Peano axioms.
When saying that 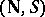 is a totally ordered set, one refers to the total order relation
is a totally ordered set, one refers to the total order relation 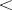 defined by:
defined by:
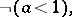 |
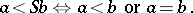 |
References
| [a1] | H.C. Kennedy, "Selected works of Giuseppe Peano" , Allen & Unwin (1973) |
| [a2] | E. Landau, "Grundlagen der Analysis" , Akad. Verlagsgesellschaft (1930) |
| [a3] | S. MacLane, "Algebra" , Macmillan (1967) |
Natural sequence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Natural_sequence&oldid=16451