Difference between revisions of "Logical matrix"
(Importing text file) |
m (link) |
||
| Line 3: | Line 3: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607401.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607401.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607402.png" /> is a non-empty set; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607403.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607404.png" /> are binary | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607402.png" /> is a non-empty set; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607403.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607404.png" /> are [[binary operation]]s; and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607405.png" /> is a [[unary operation]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607406.png" />. Any formula of propositional logic, constructed from propositional variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607407.png" /> by means of the logical connectives <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607408.png" />, can be regarded as an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l0607409.png" />-place function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074010.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074011.png" /> are assumed to be variables with range of values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074012.png" /> and the logical connectives are interpreted as the corresponding operations of the logical matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074013.png" />. A formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074014.png" /> is said to be generally valid in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074015.png" /> if for any values of the variables in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074016.png" /> the value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074017.png" /> belongs to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074018.png" />. A logical matrix <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074019.png" /> is said to be characteristic for a propositional calculus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074020.png" /> if the formulas that are generally valid in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074021.png" /> are exactly those that are deducible in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074022.png" />. An example of a logical matrix is the system |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074023.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/l/l060/l060740/l06074023.png" /></td> </tr></table> | ||
Revision as of 19:13, 13 November 2016
A system
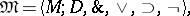 |
where 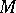 is a non-empty set;
is a non-empty set; 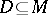 ;
; 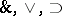 are binary operations; and
are binary operations; and  is a unary operation on
is a unary operation on 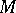 . Any formula of propositional logic, constructed from propositional variables
. Any formula of propositional logic, constructed from propositional variables  by means of the logical connectives
by means of the logical connectives 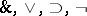 , can be regarded as an
, can be regarded as an  -place function on
-place function on 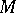 if
if  are assumed to be variables with range of values
are assumed to be variables with range of values 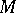 and the logical connectives are interpreted as the corresponding operations of the logical matrix
and the logical connectives are interpreted as the corresponding operations of the logical matrix 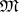 . A formula
. A formula 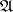 is said to be generally valid in
is said to be generally valid in 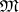 if for any values of the variables in
if for any values of the variables in 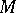 the value of
the value of  belongs to
belongs to 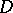 . A logical matrix
. A logical matrix 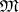 is said to be characteristic for a propositional calculus
is said to be characteristic for a propositional calculus 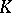 if the formulas that are generally valid in
if the formulas that are generally valid in 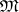 are exactly those that are deducible in
are exactly those that are deducible in 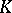 . An example of a logical matrix is the system
. An example of a logical matrix is the system
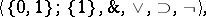 |
where
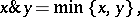 |
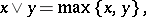 |
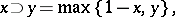 |
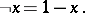 |
This logical matrix is characteristic for the classical propositional calculus. t logic','../p/p110060.htm','Set theory','../s/s084750.htm','Syntax','../s/s091900.htm','Undecidability','../u/u095140.htm','Unsolvability','../u/u095800.htm','ZFC','../z/z130100.htm')" style="background-color:yellow;">K. Gödel proved that it is impossible to construct a logical matrix with a finite set 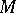 that is characteristic for the intuitionistic propositional calculus.
that is characteristic for the intuitionistic propositional calculus.
Comments
References
| [a1] | R. Wójcicki, "Theory of logical calculi" , Kluwer (1988) |
Logical matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logical_matrix&oldid=16307