Difference between revisions of "Fredholm solvability"
m (more conversions) |
m (second to last conversion) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023018.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f130/f130230/f13023018.png" /></td> </tr></table> | ||
| − | An equation $Tx=y$ is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever | + | An equation $Tx=y$ is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever $y \in (\ker T^*)^\perp $. A classical result states that $Tx=y$ is normally solvable if and only if $T(E)$ is closed in $F$. |
In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators. | In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators. | ||
Revision as of 20:08, 30 October 2016
Let $A$ be a real $(n\times n)$-matrix and $b\in R^n$ a vector.
The Fredholm alternative in $R^n$ states that the equation $Ax=b$ has a solution if and only if $b^T v =0$ for every vector $v\in R^n$ satisfying $A^T v =0$.
This alternative has many applications, e.g. in bifurcation theory. It can be generalized to abstract spaces. So, let $E$ and $F$ be Banach spaces (cf. Banach space) and let $T:E\rightarrow F$ be a continuous linear operator. Let $E^*$, respectively $F^*$, denote the topological dual of $E$, respectively $F$, and let $T^*$ denote the adjoint of $T$ (cf. also Duality; Adjoint operator). Define
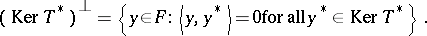 |
An equation $Tx=y$ is said to be normally solvable (in the sense of F. Hausdorff) if it has a solution whenever $y \in (\ker T^*)^\perp $. A classical result states that $Tx=y$ is normally solvable if and only if $T(E)$ is closed in $F$.
In non-linear analysis, this latter result is used as definition of normal solvability for non-linear operators.
The phrase "Fredholm solvability" refers to results and techniques for solving differential and integral equations via the Fredholm alternative and, more generally, the Fredholm-type properties of the operator involved.
References
| [a1] | F. Hausdorff, "Zur Theorie der linearen metrischen Räume" J. Reine Angew. Math. , 167 (1932) pp. 265 Zbl 0003.33104 Zbl 58.1113.05 |
| [a2] | V.A. Kozlov, V.G. Maz'ya, J. Rossmann, "Elliptic boundary value problems in domains with point singularities" , Amer. Math. Soc. (1997) MR1469972 Zbl 0947.35004 |
| [a3] | A.T. Prilepko, D.G. Orlovsky, I.A. Vasin, "Methods for solving inverse problems in mathematical physics" , M. Dekker (2000) MR1748236 Zbl 0947.35173 |
| [a4] | D.G. Orlovskij, "The Fredholm solvability of inverse problems for abstract differential equations" A.N. Tikhonov (ed.) et al. (ed.) , Ill-Posed Problems in the Natural Sciences , VSP (1992) Zbl 0789.35178 |
Fredholm solvability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fredholm_solvability&oldid=39546