Difference between revisions of "Order topology"
(Importing text file) |
m (link) |
||
| Line 12: | Line 12: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o0700809.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o0700809.png" /></td> </tr></table> | ||
| − | as a subbase for the closed sets, but in general it is different. On a complete linearly ordered set, the order topology is characterized by order convergence: that is, a net (see [[Generalized sequence|Generalized sequence]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008010.png" /> converges to a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008011.png" /> if and only if there are an increasing net <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008012.png" /> and a decreasing net <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008013.png" />, indexed by the same directed set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008014.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008015.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008017.png" />. | + | as a [[subbase]] for the closed sets, but in general it is different. On a complete linearly ordered set, the order topology is characterized by order convergence: that is, a net (see [[Generalized sequence|Generalized sequence]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008010.png" /> converges to a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008011.png" /> if and only if there are an increasing net <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008012.png" /> and a decreasing net <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008013.png" />, indexed by the same directed set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008014.png" />, such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008015.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070080/o07008017.png" />. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> O. Frink, "Topology in lattices" ''Trans. Amer. Math. Soc.'' , '''51''' (1942) pp. 569–582</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.J. Ward, "On relations between certain intrinsic topologies in partially ordered sets" ''Proc. Cambridge Philos. Soc.'' , '''51''' (1955) pp. 254–261</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> O. Frink, "Topology in lattices" ''Trans. Amer. Math. Soc.'' , '''51''' (1942) pp. 569–582</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A.J. Ward, "On relations between certain intrinsic topologies in partially ordered sets" ''Proc. Cambridge Philos. Soc.'' , '''51''' (1955) pp. 254–261</TD></TR></table> | ||
Revision as of 19:24, 19 October 2016
The topology 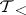 on a linearly ordered set
on a linearly ordered set 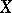 , with linear order
, with linear order  , which has a base consisting of all possible intervals of
, which has a base consisting of all possible intervals of 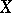 .
.
Comments
Here "interval" is used in the sense of "open interval" , i.e. a set of the form
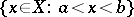 |
where 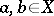 (or possibly
(or possibly 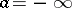 and/or
and/or 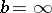 ). The order topology may be considered on partially ordered as well as linearly ordered sets; on a linearly ordered set it coincides with the interval topology which has the closed intervals
). The order topology may be considered on partially ordered as well as linearly ordered sets; on a linearly ordered set it coincides with the interval topology which has the closed intervals
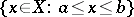 |
as a subbase for the closed sets, but in general it is different. On a complete linearly ordered set, the order topology is characterized by order convergence: that is, a net (see Generalized sequence) 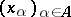 converges to a point
converges to a point  if and only if there are an increasing net
if and only if there are an increasing net 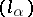 and a decreasing net
and a decreasing net 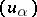 , indexed by the same directed set
, indexed by the same directed set 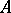 , such that
, such that 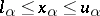 for all
for all 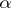 and
and 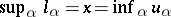 .
.
References
| [a1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [a2] | O. Frink, "Topology in lattices" Trans. Amer. Math. Soc. , 51 (1942) pp. 569–582 |
| [a3] | A.J. Ward, "On relations between certain intrinsic topologies in partially ordered sets" Proc. Cambridge Philos. Soc. , 51 (1955) pp. 254–261 |
Order topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_topology&oldid=15011