Difference between revisions of "Chinese remainder theorem"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221201.png" /> be a commutative ring with identity and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221202.png" /> be a collection of ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221203.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221204.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221205.png" />. Then, given any set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221206.png" />, there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221207.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221208.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221209.png" />. In the particular case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212010.png" /> is the ring of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212011.png" />, the Chinese remainder theorem states that for any set of pairwise coprime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212012.png" /> there is an integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212013.png" /> giving pre-assigned remainders on division by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212014.png" />. In this form the Chinese remainder theorem was known in ancient China; whence the name of the theorem. | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221201.png" /> be a commutative [[ring with identity]] and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221202.png" /> be a collection of ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221203.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221204.png" /> for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221205.png" />. Then, given any set of elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221206.png" />, there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221207.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221208.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c0221209.png" />. In the particular case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212010.png" /> is the ring of integers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212011.png" />, the Chinese remainder theorem states that for any set of pairwise coprime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212012.png" /> there is an integer <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212013.png" /> giving pre-assigned remainders on division by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212014.png" />. In this form the Chinese remainder theorem was known in ancient China; whence the name of the theorem. |
The most frequent application of the Chinese remainder theorem is in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212015.png" /> is a [[Dedekind ring|Dedekind ring]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212016.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212017.png" /> are distinct prime ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212018.png" />. (If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212019.png" /> satisfy the condition of the theorem, then so do <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212020.png" /> for any natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212021.png" />.) In this case, the Chinese remainder theorem implies that for any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212022.png" /> there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212023.png" /> such that the decomposition of the principal ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212024.png" /> into a product of prime ideals has the form | The most frequent application of the Chinese remainder theorem is in the case when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212015.png" /> is a [[Dedekind ring|Dedekind ring]] and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212016.png" />, where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212017.png" /> are distinct prime ideals in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212018.png" />. (If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212019.png" /> satisfy the condition of the theorem, then so do <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212020.png" /> for any natural numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212021.png" />.) In this case, the Chinese remainder theorem implies that for any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212022.png" /> there exists an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212023.png" /> such that the decomposition of the principal ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022120/c02212024.png" /> into a product of prime ideals has the form | ||
Revision as of 16:09, 11 September 2016
Let 
be a commutative ring with identity and let 
be a collection of ideals in 
such that 
for any 
. Then, given any set of elements 
, there exists an 
such that 
, 
. In the particular case when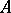 
is the ring of integers 
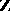, the Chinese remainder theorem states that for any set of pairwise coprime numbers 
there is an integer 
giving pre-assigned remainders on division by 
. In this form the Chinese remainder theorem was known in ancient China; whence the name of the theorem.
The most frequent application of the Chinese remainder theorem is in the case when 
is a Dedekind ring and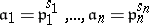 
, where the 
are distinct prime ideals in 
. (If 
satisfy the condition of the theorem, then so do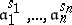 
for any natural numbers 
.) In this case, the Chinese remainder theorem implies that for any set 
there exists an 
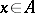such that the decomposition of the principal ideal 
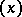into a product of prime ideals has the form
 |
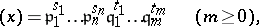where the ideals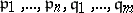 
are pairwise distinct (the theorem on the independence of exponents).
References
| [1] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) |
| [2] | S. Lang, "Algebra" , Addison-Wesley (1974) |
| [3] | S. Lang, "Algebraic numbers" , Addison-Wesley (1964) |
How to Cite This Entry:
Chinese remainder theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chinese_remainder_theorem&oldid=11578
Chinese remainder theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chinese_remainder_theorem&oldid=11578
This article was adapted from an original article by L.V. Kuz'min (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article