Difference between revisions of "Golden ratio"
(asy code to subpage) |
m (mark tex done) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''golden section, sectio aurea, sectio divina, divina proportio, golden mean, harmonic division, division in extreme and mean ratio'' | ''golden section, sectio aurea, sectio divina, divina proportio, golden mean, harmonic division, division in extreme and mean ratio'' | ||
| − | The division of a line segment | + | The division of a line segment $a$ into two parts the greater of which, $x$, is the mean proportional between the whole segment $a$ and the smaller part $a-x$, i.e. |
| − | + | \[ | |
| − | + | \label{ratio} | |
| − | + | a : x = x : (a-x). | |
| − | + | \] | |
| − | |||
| − | |||
| + | To find $x$, one has to solve a quadratic equation, | ||
| + | \[ | ||
| + | x^2+ax-a^2 = 0, | ||
| + | \] | ||
the positive solution of which is | the positive solution of which is | ||
| − | + | \[ | |
| + | x = \frac{-1+\sqrt{5}}{2} a \approx 0.62 a. | ||
| + | \] | ||
| − | Condition | + | Condition \eqref{ratio} may also be written as |
| − | + | \[ | |
| + | \frac{x}{a}\left(1+\frac{x}{a}\right) = 1 \quad \text{or} \quad x = \frac{a}{1+\frac{x}{a}} | ||
| + | \] | ||
or | or | ||
| + | \[ | ||
| + | x = a \frac{ 1}{ 1+ \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \ldots}}} }, | ||
| + | \] | ||
| − | + | i.e. representing $x$ as a continued fraction, the convergents of which are | |
| − | |||
| − | i.e. representing | ||
| − | + | \[ | |
| + | \frac{1}{1}, \frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}, \frac{8}{13}, \frac{13}{21}, \text{etc.}, | ||
| + | \] | ||
| − | where | + | where $1,1,2,3,5,8,13,21,\ldots,$ are the [[Fibonacci numbers|Fibonacci numbers]]. |
{{:Golden ratio/Fig1}} | {{:Golden ratio/Fig1}} | ||
| − | The golden ratio of a segment | + | The golden ratio of a segment $AB$ may be found by a geometric construction (see Fig.). Draw the perpendicular to $AB$ at $B$; on the perpendicular, mark off the segment $BE=AB/2$; then join $A$ and $E$, mark off $ED=EB$ and finally $AC=AD$. Then |
| − | + | \[ | |
| + | AB:AC=AC:CB . | ||
| + | \] | ||
The golden ratio was already known in Antiquity. Its first appearance in the extant classical literature is in Euclid's Elements, Book II, 11 (3th century B.C.). | The golden ratio was already known in Antiquity. Its first appearance in the extant classical literature is in Euclid's Elements, Book II, 11 (3th century B.C.). | ||
Latest revision as of 21:24, 3 April 2015
golden section, sectio aurea, sectio divina, divina proportio, golden mean, harmonic division, division in extreme and mean ratio
The division of a line segment $a$ into two parts the greater of which, $x$, is the mean proportional between the whole segment $a$ and the smaller part $a-x$, i.e. \[ \label{ratio} a : x = x : (a-x). \]
To find $x$, one has to solve a quadratic equation, \[ x^2+ax-a^2 = 0, \] the positive solution of which is
\[ x = \frac{-1+\sqrt{5}}{2} a \approx 0.62 a. \]
Condition \eqref{ratio} may also be written as
\[ \frac{x}{a}\left(1+\frac{x}{a}\right) = 1 \quad \text{or} \quad x = \frac{a}{1+\frac{x}{a}} \]
or \[ x = a \frac{ 1}{ 1+ \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \ldots}}} }, \]
i.e. representing $x$ as a continued fraction, the convergents of which are
\[ \frac{1}{1}, \frac{1}{2}, \frac{2}{3}, \frac{3}{5}, \frac{5}{8}, \frac{8}{13}, \frac{13}{21}, \text{etc.}, \]
where $1,1,2,3,5,8,13,21,\ldots,$ are the Fibonacci numbers.
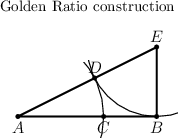
The golden ratio of a segment $AB$ may be found by a geometric construction (see Fig.). Draw the perpendicular to $AB$ at $B$; on the perpendicular, mark off the segment $BE=AB/2$; then join $A$ and $E$, mark off $ED=EB$ and finally $AC=AD$. Then
\[ AB:AC=AC:CB . \]
The golden ratio was already known in Antiquity. Its first appearance in the extant classical literature is in Euclid's Elements, Book II, 11 (3th century B.C.).
Principles based on the golden ratio or similar proportional ratios provided the basis for the compositional design of many works of art (mainly architectural works of Antiquity and the Renaissance).
Comments
The golden ratio occurs in many places in nature. It is assumed to have been known and used by the Pythagoreans (500 B.C.).
The term "divina proportio" (sectio divina, divine section) has been introduced by Fra Luca Pacioli in his book: De Divina Proportione (1509). Later on he collaborated with Leonardo da Vinci on this topic. The term "golden section" (sectio aurea) is from a later date (probably 18th century).
Golden ratio. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Golden_ratio&oldid=35614