Difference between revisions of "Combinatorial geometry(2)"
(Importing text file) |
m (link) |
||
| Line 3: | Line 3: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232702.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232702.png" /></td> </tr></table> | ||
| − | defined for all subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232703.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232704.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232705.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232706.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232707.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232708.png" />, but not necessarily <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232709.png" />), and satisfying the conditions: 1) for the empty set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327010.png" />; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327011.png" /> for each element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327012.png" />; and 3) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327014.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327015.png" /> but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327016.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327017.png" /> (the "exchange" property). The closed sets, or subspaces, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327018.png" /> form a geometric lattice (cf. [[Semi-Dedekind lattice|Semi-Dedekind lattice]]). A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327019.png" /> is independent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327020.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327021.png" />; all maximal independent sets, or bases, have the same cardinality. The direct sum of combinatorial geometries and the restriction of a combinatorial geometry to a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327022.png" /> are defined in the usual way. The cardinality of the bases of the restriction of a combinatorial geometry to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327023.png" /> is called the rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327025.png" />. The rank function satisfies the condition | + | defined for all subsets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232703.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232704.png" /> (that is, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232705.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232706.png" /> implies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232707.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232708.png" />, but not necessarily <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c0232709.png" />), and satisfying the conditions: 1) for the empty set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327010.png" />; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327011.png" /> for each element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327012.png" />; and 3) if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327014.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327015.png" /> but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327016.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327017.png" /> (the "exchange" property). The closed sets, or subspaces, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327018.png" /> form a [[geometric lattice]] (cf. [[Semi-Dedekind lattice|Semi-Dedekind lattice]]). A subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327019.png" /> is independent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327020.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327021.png" />; all maximal independent sets, or bases, have the same cardinality. The direct sum of combinatorial geometries and the restriction of a combinatorial geometry to a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327022.png" /> are defined in the usual way. The cardinality of the bases of the restriction of a combinatorial geometry to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327023.png" /> is called the rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327024.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327025.png" />. The rank function satisfies the condition |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327026.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c023/c023270/c02327026.png" /></td> </tr></table> | ||
Revision as of 21:14, 3 January 2015
A finite set 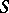 together with a closure relation
together with a closure relation
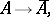 |
defined for all subsets 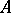 of
of 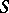 (that is,
(that is, 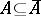 ,
, 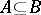 implies
implies 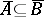 and
and 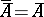 , but not necessarily
, but not necessarily 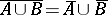 ), and satisfying the conditions: 1) for the empty set
), and satisfying the conditions: 1) for the empty set  ; 2)
; 2) 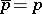 for each element
for each element 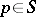 ; and 3) if
; and 3) if 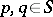 and
and 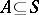 and if
and if 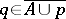 but
but 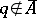 , then
, then 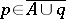 (the "exchange" property). The closed sets, or subspaces,
(the "exchange" property). The closed sets, or subspaces, 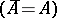 form a geometric lattice (cf. Semi-Dedekind lattice). A subset
form a geometric lattice (cf. Semi-Dedekind lattice). A subset 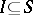 is independent if
is independent if 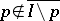 for all
for all 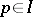 ; all maximal independent sets, or bases, have the same cardinality. The direct sum of combinatorial geometries and the restriction of a combinatorial geometry to a subset
; all maximal independent sets, or bases, have the same cardinality. The direct sum of combinatorial geometries and the restriction of a combinatorial geometry to a subset 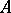 are defined in the usual way. The cardinality of the bases of the restriction of a combinatorial geometry to
are defined in the usual way. The cardinality of the bases of the restriction of a combinatorial geometry to 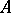 is called the rank
is called the rank 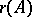 of
of 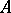 . The rank function satisfies the condition
. The rank function satisfies the condition
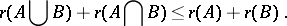 |
A subset 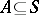 for which
for which 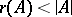 is said to be dependent; the minimal dependent sets of a combinatorial geometry are called circuits. By dropping conditions 1) and 2) in the definition of a combinatorial geometry one obtains the definition of a pre-geometry or matroid. Infinite combinatorial geometries are also considered, but here it is required that the bases be finite.
is said to be dependent; the minimal dependent sets of a combinatorial geometry are called circuits. By dropping conditions 1) and 2) in the definition of a combinatorial geometry one obtains the definition of a pre-geometry or matroid. Infinite combinatorial geometries are also considered, but here it is required that the bases be finite.
Example of a combinatorial geometry. A subset 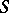 of a vector space
of a vector space 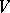 with the relation
with the relation
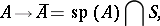 |
defined for all 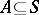 , where
, where 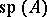 is the linear subspace in
is the linear subspace in 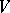 spanned by
spanned by 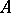 .
.
One of the fundamental problems in the theory of combinatorial geometries is the so-called critical problem. For the combinatorial geometry defined by a set 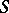 in an
in an  -dimensional projective space over a Galois field, this problem consists in the determination of the smallest positive integer
-dimensional projective space over a Galois field, this problem consists in the determination of the smallest positive integer 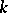 (the critical exponent) for which there exists a family of hyperplanes
(the critical exponent) for which there exists a family of hyperplanes 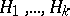 distinguishing
distinguishing 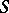 . (A family of hyperplanes distinguishes a set
. (A family of hyperplanes distinguishes a set 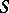 if for every
if for every 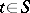 there is at least one hyperplane not containing
there is at least one hyperplane not containing 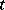 .)
.)
References
| [1] | H. Whitney, "On the abstract properties of linear dependence" Amer. J. Math. , 57 (1935) pp. 509–533 |
| [2] | H.H. Crapo, G.C. Rota, "On the foundations of combinatorial theory: combinatorial geometries" , M.I.T. (1970) |
| [3] | W.T. Tutte, "Introduction to the theory of matroids" , American Elsevier (1971) |
| [4] | R.J. Wilson, "Introduction to graph theory" , Oliver & Boyd (1972) |
| [5] | K.A. Rybnikov, "Introduction to combinatorial analysis" , Moscow (1972) (In Russian) |
| [6] | D.J.A. Welsh, "Matroid theory" , Acad. Press (1976) |
| [7] | R. von Randow, "Introduction to the theory of matroids" , Springer (1975) |
| [8] | N. White (ed.) , Theory of matroids , Cambridge Univ. Press (1986) |
| [9] | K.A. Rybnikov (ed.) , Combinatorial analysis: exercises and problems , Moscow (1982) (In Russian) |
Combinatorial geometry(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Combinatorial_geometry(2)&oldid=15806