Difference between revisions of "Everett interpolation formula"
(→References: Everett (1900)) |
(This is throwback, due to L. J. Comrie) |
||
| Line 25: | Line 25: | ||
and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665017.png" /> is used to find both values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665018.png" />. | and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665017.png" /> is used to find both values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665018.png" />. | ||
| − | + | For manual calculation in the case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665019.png" />, L. J. Comrie introduced '''throwback'''. It is advisable to approximate the coefficient of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665020.png" /> in (2) by | |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036650/e03665021.png" /></td> </tr></table> | ||
| Line 44: | Line 44: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
| Line 55: | Line 58: | ||
<TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126</TD></TR> | <TR><TD valign="top">[a1]</TD> <TD valign="top"> P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126</TD></TR> | ||
<TR><TD valign="top">[a2]</TD> <TD valign="top"> A.J. Thomson, "Table of the coefficients of Everett's central difference interpolation formula" , Cambridge Univ. Press (1965)</TD></TR> | <TR><TD valign="top">[a2]</TD> <TD valign="top"> A.J. Thomson, "Table of the coefficients of Everett's central difference interpolation formula" , Cambridge Univ. Press (1965)</TD></TR> | ||
| − | <TR><TD valign="top">[b1]</TD> <TD valign="top"> J. D. Everett, "On interpolation formulae", ''Quarterly J.'' '''32''' (1900) 306-313 {{ZBL|32.0271.01}}</TD></TR> | + | <TR><TD valign="top">[b1]</TD> <TD valign="top"> L. J. Comrie, "Inverse interpolation and scientific applications of the national accounting machine", Suppl. JR statist. Soc. London '''3''' (1936) 87-114 {{ZBL|63.1136.02}}}</TD></TR> |
| − | <TR><TD valign="top">[ | + | <TR><TD valign="top">[b2]</TD> <TD valign="top"> J. D. Everett, "On interpolation formulae", ''Quarterly J.'' '''32''' (1900) 306-313 {{ZBL|32.0271.01}}</TD></TR> |
| + | <TR><TD valign="top">[b3]</TD> <TD valign="top"> Maurice V. Wilkes, "A short introduction to numerical analysis", Cambridge University Press (1966) ISBN 0-521-09412-7 {{ZBL|0149.10902}}</TD</TR> | ||
</table> | </table> | ||
Revision as of 16:40, 3 January 2015
A method of writing the interpolation polynomial obtained from the Gauss interpolation formula for forward interpolation at 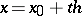 with respect to the nodes
with respect to the nodes 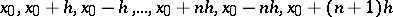 , that is,
, that is,
 |
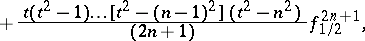 |
without finite differences of odd order, which are eliminated by means of the relation
 |
Adding like terms yields Everett's interpolation formula
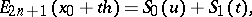 | (1) |
where 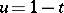 and
and
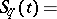 | (2) |
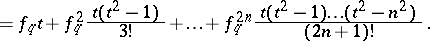 |
Compared with other versions of the interpolation polynomial, formula (1) reduces approximately by half the amount of work required to solve the problem of table condensation; for example, when a given table of the values of a function at 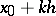 is to be used to draw up a table of the values of the same function at
is to be used to draw up a table of the values of the same function at 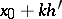 ,
, 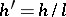 , where
, where 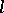 is an integer, the values
is an integer, the values 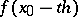 for
for 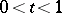 are computed be means of the formula
are computed be means of the formula
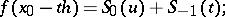 |
and 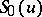 is used to find both values
is used to find both values 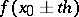 .
.
For manual calculation in the case 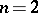 , L. J. Comrie introduced throwback. It is advisable to approximate the coefficient of
, L. J. Comrie introduced throwback. It is advisable to approximate the coefficient of 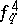 in (2) by
in (2) by
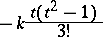 |
and instead of 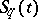 to compute
to compute
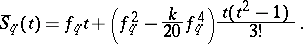 |
The parameter 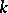 can be chosen, for example, from the condition that the principal part of
can be chosen, for example, from the condition that the principal part of
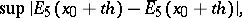 |
where
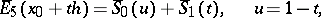 |
has a minimum value. In this case 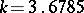 .
.
References
| [1] | I.S. Berezin, N.P. Zhidkov, "Computing methods" , Pergamon (1973) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
Comments
References
| [a1] | P.J. Davis, "Interpolation and approximation" , Dover, reprint (1975) pp. 108–126 |
| [a2] | A.J. Thomson, "Table of the coefficients of Everett's central difference interpolation formula" , Cambridge Univ. Press (1965) |
| [b1] | L. J. Comrie, "Inverse interpolation and scientific applications of the national accounting machine", Suppl. JR statist. Soc. London 3 (1936) 87-114 Zbl 63.1136.02} |
| [b2] | J. D. Everett, "On interpolation formulae", Quarterly J. 32 (1900) 306-313 Zbl 32.0271.01 |
| [b3] | Maurice V. Wilkes, "A short introduction to numerical analysis", Cambridge University Press (1966) ISBN 0-521-09412-7 Zbl 0149.10902</TD |
Everett interpolation formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Everett_interpolation_formula&oldid=36054