Difference between revisions of "Catalan constant"
(→Euler–Mascheroni constant.: moved text to Euler constant) |
(References: Finch (2003)) |
||
| Line 70: | Line 70: | ||
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004032.png" /> denotes the familiar [[Riemann zeta-function|Riemann zeta-function]]. | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c130/c130040/c13004032.png" /> denotes the familiar [[Riemann zeta-function|Riemann zeta-function]]. | ||
| + | |||
| + | ====References==== | ||
| + | {| | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Fi}}||valign="top"| Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications '''94''', Cambridge University Press (2003) ISBN 0-521-81805-2 {{ZBL|1054.00001}} | ||
| + | |- | ||
| + | |} | ||
Revision as of 19:08, 29 December 2014
Named after its inventor, E.Ch. Catalan (1814–1894), the Catalan constant 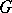 (which is denoted also by
(which is denoted also by 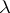 ) is defined by
) is defined by
 | (a1) |
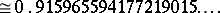 |
If, in terms of the Digamma (or Psi) function 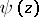 , defined by
, defined by
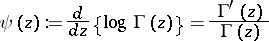 | (a2) |
or
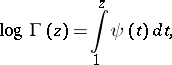 |
one puts
 | (a3) |
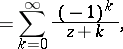 |
where
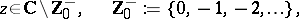 |
then
 | (a4) |
which provides a relationship between the Catalan constant 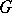 and the Digamma function
and the Digamma function 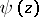 .
.
The Catalan constant 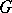 is related also to other functions, such as the Clausen function
is related also to other functions, such as the Clausen function 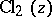 , defined by
, defined by
 | (a5) |
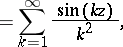 |
and the Hurwitz zeta-function 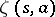 , which is defined, when
, which is defined, when 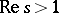 , by
, by
 | (a6) |
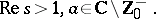 |
Thus,
 | (a7) |
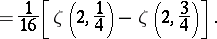 |
Since
 | (a8) |
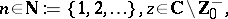 |
the last expression in (a7) would follow also from (a4) in light of the definition in (a3).
A fairly large number of integrals and series can be evaluated in terms of the Catalan constant 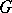 . For example,
. For example,
 | (a9) |
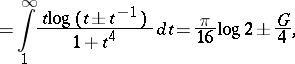 |
 | (a10) |
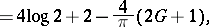 |
and
 | (a11) |
where 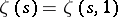 denotes the familiar Riemann zeta-function.
denotes the familiar Riemann zeta-function.
References
| [Fi] | Steven R. Finch, "Mathematical constants" , Encyclopedia of mathematics and its applications 94, Cambridge University Press (2003) ISBN 0-521-81805-2 Zbl 1054.00001 |
Catalan constant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Catalan_constant&oldid=35952