Difference between revisions of "Ordered sum"
From Encyclopedia of Mathematics
(Importing text file) |
m (links) |
||
| Line 1: | Line 1: | ||
''of partially ordered sets'' | ''of partially ordered sets'' | ||
| − | An operation which associates with a system of disjoint partially ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701701.png" />, where the index set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701702.png" /> is also partially ordered, a new [[ | + | An operation which associates with a system of disjoint partially ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701701.png" />, where the index set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701702.png" /> is also partially ordered, a new [[partially ordered set]] |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701703.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701703.png" /></td> </tr></table> | ||
| − | the elements of which are the elements of the set-theoretical union of the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701704.png" />, with order defined as follows. On the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701705.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701706.png" /> if and only if either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701707.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701708.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701709.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017012.png" />. Important particular cases of ordered sums are the cardinal and ordinal sums. The first of these is obtained when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017013.png" /> is trivially ordered, i.e. each of its elements is comparable only to itself, and the second when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017014.png" /> is a [[Totally ordered set|totally ordered set]]. Thus, in the cardinal sum of two disjoint partially ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017016.png" /> the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017017.png" /> retains its meaning in the components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017019.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017021.png" /> are incomparable; in the ordinal sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017023.png" /> the order relation is again preserved in the components and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017024.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017026.png" />. | + | the elements of which are the elements of the set-theoretical [[disjoint union]] of the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701704.png" />, with order defined as follows. On the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701705.png" /> one has <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701706.png" /> if and only if either <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701707.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701708.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o0701709.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017010.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017011.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017012.png" />. Important particular cases of ordered sums are the cardinal and ordinal sums. The first of these is obtained when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017013.png" /> is trivially ordered, i.e. each of its elements is comparable only to itself, and the second when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017014.png" /> is a [[Totally ordered set|totally ordered set]]. Thus, in the cardinal sum of two disjoint partially ordered sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017015.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017016.png" /> the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017017.png" /> retains its meaning in the components <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017018.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017019.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017021.png" /> are incomparable; in the ordinal sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017022.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017023.png" /> the order relation is again preserved in the components and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017024.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o070/o070170/o07017026.png" />. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> G. Birkhoff, "Lattice theory" , ''Colloq. Publ.'' , '''25''' , Amer. Math. Soc. (1973)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian)</TD></TR> | ||
| + | </table> | ||
Revision as of 18:57, 6 December 2014
of partially ordered sets
An operation which associates with a system of disjoint partially ordered sets 
, where the index set 
is also partially ordered, a new partially ordered set
 |
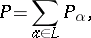the elements of which are the elements of the set-theoretical disjoint union of the sets 
, with order defined as follows. On the set 
one has 
if and only if either 
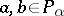and 
in 
or 
, 
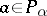and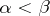 
. Important particular cases of ordered sums are the cardinal and ordinal sums. The first of these is obtained when 
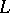is trivially ordered, i.e. each of its elements is comparable only to itself, and the second when 
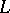is a totally ordered set. Thus, in the cardinal sum of two disjoint partially ordered sets 
and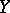 
the relation 
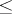retains its meaning in the components 
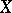and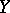 
, while 
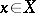and 
are incomparable; in the ordinal sum of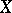 
and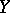 
the order relation is again preserved in the components and 
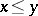for all 
, 
.
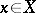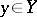References
| [1] | G. Birkhoff, "Lattice theory" , Colloq. Publ. , 25 , Amer. Math. Soc. (1973) |
| [2] | L.A. Skornyakov, "Elements of lattice theory" , Hindushtan Publ. Comp. (1977) (Translated from Russian) |
How to Cite This Entry:
Ordered sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_sum&oldid=14587
Ordered sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ordered_sum&oldid=14587
This article was adapted from an original article by T.S. Fofanova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article