Difference between revisions of "Matrix Viète theorem"
Ulf Rehmann (talk | contribs) m (moved Matrix Viete theorem to Matrix Viète theorem over redirect: accented title) |
m (link) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201701.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201701.png" /></td> <td valign="top" style="width:5%;text-align:right;">(a1)</td></tr></table> | ||
| − | in terms of the roots: up to sign, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201702.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201703.png" />th elementary symmetric function of the roots <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201704.png" />. See also [[Viète theorem|Viète theorem]]. | + | in terms of the roots: up to sign, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201702.png" /> is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201703.png" />th [[elementary symmetric function]] of the roots <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m120/m120170/m1201704.png" />. See also [[Viète theorem|Viète theorem]]. |
Consider now a matrix equation | Consider now a matrix equation | ||
Revision as of 18:24, 4 December 2014
matrix Vieta theorem
The standard (scalar) Viète formulas express the coefficients of an equation
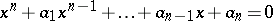 | (a1) |
in terms of the roots: up to sign,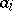 
is the 
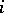th elementary symmetric function of the roots 
. See also Viète theorem.
Consider now a matrix equation
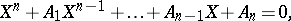 | (a2) |
where the solutions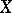 
and coefficients 
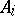are square complex matrices. A set of 
square matrices 
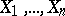of size 
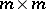is called independent if the block Vandermonde determinant
 |
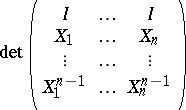does not vanish. The matrix Viète theorem gives formulas for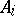 
in terms of quasi-determinants, [a3], [a4], involving 
independent solutions of (a2), [a1], [a2]. In particular, if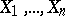 
are 
independent solutions of (a2), then
 |
 |
 |
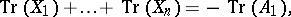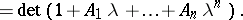This theorem generalizes to the case of equations in an arbitrary associative ring (cf. also Associative rings and algebras), with an adequate notion of trace and determinant, see [a1], [a2].
References
| [a1] | A. Connes, A. Schwarz, "Matrix Vieta theorem revisited" Lett. Math. Phys. , 39 : 4 (1997) pp. 349–353 |
| [a2] | D. Fuchs, A. Schwarz, "Matrix Vieta theorem" Amer. Math. Soc. Transl. (2) , 169 (1995) pp. 15–22 |
| [a3] | I.M. Gel'fand, D. Krob, A. Lascoux, B. Leclerc, V.S. Redakh, J.Y. Thibon, "Noncomutative symmetric functions" Adv. Math. , 112 (1995) pp. 218–348 |
| [a4] | I.M. Gel'fand, V.S. Redakh, "A theory of noncommutative determinants and characteristic functions of graphs I" Publ. LACIM (Univ. Quebec) , 14 pp. 1–26 |
Matrix Viète theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matrix_Vi%C3%A8te_theorem&oldid=23412