Difference between revisions of "Bimodule"
From Encyclopedia of Mathematics
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
''double module'' | ''double module'' | ||
| − | An Abelian group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163101.png" /> that is a left module over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163102.png" /> and a right module over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163103.png" />, and is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163104.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163107.png" />. One says that this is the situation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163108.png" />, or that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163109.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631010.png" />-bimodule. The bimodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631011.png" /> may be regarded as a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631012.png" />-module, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631013.png" /> is the ring | + | An Abelian group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163101.png" /> that is a left module over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163102.png" /> and a right module over a ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163103.png" />, and is such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163104.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163105.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163106.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163107.png" />. One says that this is the situation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163108.png" />, or that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b0163109.png" /> is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631010.png" />-bimodule. The bimodule <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631011.png" /> may be regarded as a left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631012.png" />-module, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631013.png" /> is the [[opposite ring]] (dually isomorphic, anti-isomorphic) to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631014.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631015.png" /> denotes the tensor product over the ring of integers, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631016.png" />. For every left <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631017.png" />-module <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631018.png" /> one has the situation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631019.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631020.png" /> is the ring of endomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631021.png" />. Any ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631022.png" /> can be given the natural structure of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016310/b01631023.png" />-bimodule. |
Revision as of 22:29, 30 November 2014
double module
An Abelian group 
that is a left module over a ring 
and a right module over a ring 
, and is such that 
for all 
, 
, 
. One says that this is the situation 
, or that 
is an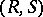 
-bimodule. The bimodule 
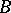may be regarded as a left 
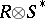-module, where 
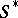is the opposite ring (dually isomorphic, anti-isomorphic) to 
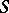, while 
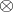denotes the tensor product over the ring of integers, and 
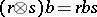. For every left 
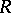-module 
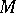one has the situation 
, where 
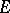is the ring of endomorphisms of 
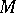. Any ring 
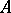can be given the natural structure of an 
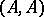-bimodule.
Comments
A bimodule morphism is a mapping from a bimodule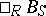 
into a bimodule 
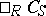that is left 
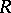-linear and right 
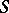-linear. The category of 
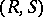-bimodules with bimodule morphisms is a Grothendieck category.
The centre of an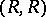 
-bimodule (also called an 
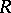-bimodule) 
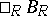is defined to be the set 
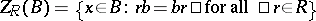. Clearly 
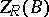is a two-sided 
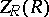-module.
How to Cite This Entry:
Bimodule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bimodule&oldid=13998
Bimodule. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Bimodule&oldid=13998
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article