Difference between revisions of "Hilbert algebra"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
An algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472301.png" /> with involution (cf. [[Involution algebra|Involution algebra]]) over the field of complex numbers, equipped with a non-degenerate scalar product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472302.png" />, for which the following axioms are satisfied: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472303.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472304.png" />; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472305.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472306.png" />; 3) for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472307.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472308.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472309.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723010.png" /> is continuous; and 4) the set of elements of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723012.png" />, is everywhere dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723013.png" />. Examples of Hilbert algebras include the algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723014.png" /> (with respect to convolution), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723015.png" /> is a compact topological group, and the algebra of Hilbert–Schmidt operators (cf. [[Hilbert–Schmidt operator|Hilbert–Schmidt operator]]) on a given Hilbert space. | An algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472301.png" /> with involution (cf. [[Involution algebra|Involution algebra]]) over the field of complex numbers, equipped with a non-degenerate scalar product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472302.png" />, for which the following axioms are satisfied: 1) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472303.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472304.png" />; 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472305.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472306.png" />; 3) for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472307.png" /> the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472308.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h0472309.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723010.png" /> is continuous; and 4) the set of elements of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723011.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723012.png" />, is everywhere dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723013.png" />. Examples of Hilbert algebras include the algebras <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723014.png" /> (with respect to convolution), where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723015.png" /> is a compact topological group, and the algebra of Hilbert–Schmidt operators (cf. [[Hilbert–Schmidt operator|Hilbert–Schmidt operator]]) on a given Hilbert space. | ||
| − | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723016.png" /> be a Hilbert algebra, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723017.png" /> be the [[Hilbert space|Hilbert space]] completion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723018.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723020.png" /> be the elements of the algebra of bounded linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723021.png" /> which are the continuous extensions of the multiplications from the left and from the right by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723022.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723023.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723024.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723025.png" />) is a non-degenerate representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723026.png" /> (respectively, of the opposite algebra), on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723027.png" />. The weak closure of the family of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723028.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723029.png" />) is a [[Von Neumann algebra|von Neumann algebra]] in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723030.png" />; it is called the left (respectively, right) von Neumann algebra of the given Hilbert algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723031.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723032.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723033.png" />); <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723035.png" /> are mutual commutators; they are semi-finite von Neumann algebras. Any Hilbert algebra unambiguously determines some specific normal semi-finite trace on the von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723036.png" /> (cf. [[Trace on a C*-algebra|Trace on a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723037.png" />-algebra]]). Conversely, if a von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723038.png" /> and a specific semi-finite trace on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723039.png" /> are given, then it is possible to construct a Hilbert algebra such that the left von Neumann algebra of this Hilbert algebra is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723040.png" /> and the trace determined by the Hilbert algebra on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723041.png" /> coincides with the initial one [[#References|[1]]]. Thus, a Hilbert algebra is a means of studying semi-finite von Neumann algebras and traces on them; a certain extension of the concept of a Hilbert algebra makes it possible to study by similar means von Neumann algebras that are not necessarily semi-finite [[#References|[2]]]. | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723016.png" /> be a Hilbert algebra, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723017.png" /> be the [[Hilbert space|Hilbert space]] completion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723018.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723020.png" /> be the elements of the algebra of bounded linear operators on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723021.png" /> which are the continuous extensions of the multiplications from the left and from the right by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723022.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723023.png" />. The mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723024.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723025.png" />) is a non-degenerate representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723026.png" /> (respectively, of the [[opposite algebra]]), on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723027.png" />. The weak closure of the family of operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723028.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723029.png" />) is a [[Von Neumann algebra|von Neumann algebra]] in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723030.png" />; it is called the left (respectively, right) von Neumann algebra of the given Hilbert algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723031.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723032.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723033.png" />); <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723035.png" /> are mutual commutators; they are semi-finite von Neumann algebras. Any Hilbert algebra unambiguously determines some specific normal semi-finite trace on the von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723036.png" /> (cf. [[Trace on a C*-algebra|Trace on a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723037.png" />-algebra]]). Conversely, if a von Neumann algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723038.png" /> and a specific semi-finite trace on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723039.png" /> are given, then it is possible to construct a Hilbert algebra such that the left von Neumann algebra of this Hilbert algebra is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723040.png" /> and the trace determined by the Hilbert algebra on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h047/h047230/h04723041.png" /> coincides with the initial one [[#References|[1]]]. Thus, a Hilbert algebra is a means of studying semi-finite von Neumann algebras and traces on them; a certain extension of the concept of a Hilbert algebra makes it possible to study by similar means von Neumann algebras that are not necessarily semi-finite [[#References|[2]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "Les algèbres d'opérateurs dans l'espace hilbertien: algèbres de von Neumann" , Gauthier-Villars (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Takesaki, "Tomita's theory of modular Hilbert algebras and its applications" , ''Lect. notes in math.'' , '''128''' , Springer (1970)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Dixmier, "Les algèbres d'opérateurs dans l'espace hilbertien: algèbres de von Neumann" , Gauthier-Villars (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Takesaki, "Tomita's theory of modular Hilbert algebras and its applications" , ''Lect. notes in math.'' , '''128''' , Springer (1970)</TD></TR></table> | ||
Revision as of 21:58, 29 November 2014
An algebra 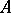 with involution (cf. Involution algebra) over the field of complex numbers, equipped with a non-degenerate scalar product
with involution (cf. Involution algebra) over the field of complex numbers, equipped with a non-degenerate scalar product 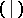 , for which the following axioms are satisfied: 1)
, for which the following axioms are satisfied: 1) 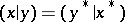 for all
for all 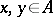 ; 2)
; 2) 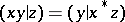 for all
for all 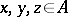 ; 3) for all
; 3) for all 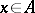 the mapping
the mapping 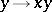 of
of 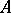 into
into 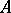 is continuous; and 4) the set of elements of the form
is continuous; and 4) the set of elements of the form 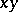 ,
, 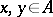 , is everywhere dense in
, is everywhere dense in 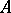 . Examples of Hilbert algebras include the algebras
. Examples of Hilbert algebras include the algebras 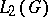 (with respect to convolution), where
(with respect to convolution), where 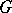 is a compact topological group, and the algebra of Hilbert–Schmidt operators (cf. Hilbert–Schmidt operator) on a given Hilbert space.
is a compact topological group, and the algebra of Hilbert–Schmidt operators (cf. Hilbert–Schmidt operator) on a given Hilbert space.
Let 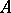 be a Hilbert algebra, let
be a Hilbert algebra, let 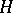 be the Hilbert space completion of
be the Hilbert space completion of 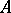 and let
and let 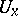 and
and 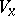 be the elements of the algebra of bounded linear operators on
be the elements of the algebra of bounded linear operators on 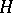 which are the continuous extensions of the multiplications from the left and from the right by
which are the continuous extensions of the multiplications from the left and from the right by  in
in 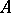 . The mapping
. The mapping 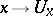 (respectively,
(respectively, 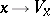 ) is a non-degenerate representation of
) is a non-degenerate representation of 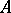 (respectively, of the opposite algebra), on
(respectively, of the opposite algebra), on 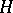 . The weak closure of the family of operators
. The weak closure of the family of operators 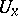 (respectively,
(respectively, 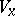 ) is a von Neumann algebra in
) is a von Neumann algebra in 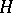 ; it is called the left (respectively, right) von Neumann algebra of the given Hilbert algebra
; it is called the left (respectively, right) von Neumann algebra of the given Hilbert algebra 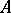 and is denoted by
and is denoted by 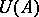 (respectively,
(respectively, 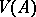 );
); 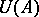 and
and 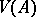 are mutual commutators; they are semi-finite von Neumann algebras. Any Hilbert algebra unambiguously determines some specific normal semi-finite trace on the von Neumann algebra
are mutual commutators; they are semi-finite von Neumann algebras. Any Hilbert algebra unambiguously determines some specific normal semi-finite trace on the von Neumann algebra 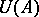 (cf. Trace on a
(cf. Trace on a 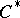 -algebra). Conversely, if a von Neumann algebra
-algebra). Conversely, if a von Neumann algebra 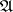 and a specific semi-finite trace on
and a specific semi-finite trace on 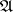 are given, then it is possible to construct a Hilbert algebra such that the left von Neumann algebra of this Hilbert algebra is isomorphic to
are given, then it is possible to construct a Hilbert algebra such that the left von Neumann algebra of this Hilbert algebra is isomorphic to 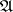 and the trace determined by the Hilbert algebra on
and the trace determined by the Hilbert algebra on 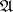 coincides with the initial one [1]. Thus, a Hilbert algebra is a means of studying semi-finite von Neumann algebras and traces on them; a certain extension of the concept of a Hilbert algebra makes it possible to study by similar means von Neumann algebras that are not necessarily semi-finite [2].
coincides with the initial one [1]. Thus, a Hilbert algebra is a means of studying semi-finite von Neumann algebras and traces on them; a certain extension of the concept of a Hilbert algebra makes it possible to study by similar means von Neumann algebras that are not necessarily semi-finite [2].
References
| [1] | J. Dixmier, "Les algèbres d'opérateurs dans l'espace hilbertien: algèbres de von Neumann" , Gauthier-Villars (1957) |
| [2] | M. Takesaki, "Tomita's theory of modular Hilbert algebras and its applications" , Lect. notes in math. , 128 , Springer (1970) |
Hilbert algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hilbert_algebra&oldid=18758