Difference between revisions of "Néron model"
Ulf Rehmann (talk | contribs) m (moved Neron model to Néron model over redirect: accented title) |
m (links) |
||
| Line 1: | Line 1: | ||
''of an Abelian variety'' | ''of an Abelian variety'' | ||
| − | A [[Group scheme|group scheme]] associated to an [[Abelian variety|Abelian variety]] and having a certain minimality property. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662901.png" /> is a local Henselian discrete valuation ring with residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662902.png" /> and field of fractions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662903.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662904.png" /> is an Abelian variety of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662905.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662906.png" />, then a Néron model of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662907.png" /> is defined as a smooth commutative group scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662908.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662909.png" /> whose generic fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629010.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629011.png" />, while the canonical homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629012.png" /> is an isomorphism. This concept was introduced by A. Néron [[#References|[1]]] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629013.png" />-isomorphism. A Néron model has the following minimality property: For any smooth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629014.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629015.png" /> and any morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629016.png" /> of the generic fibres there exists a unique morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629017.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629018.png" />-schemes induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629019.png" />. | + | A [[Group scheme|group scheme]] associated to an [[Abelian variety|Abelian variety]] and having a certain minimality property. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662901.png" /> is a local Henselian [[discrete valuation ring]] with residue field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662902.png" /> and [[field of fractions]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662903.png" /> and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662904.png" /> is an Abelian variety of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662905.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662906.png" />, then a Néron model of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662907.png" /> is defined as a smooth commutative group scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662908.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n0662909.png" /> whose generic fibre <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629010.png" /> is isomorphic to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629011.png" />, while the canonical homomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629012.png" /> is an isomorphism. This concept was introduced by A. Néron [[#References|[1]]] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629013.png" />-isomorphism. A Néron model has the following minimality property: For any smooth <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629014.png" />-scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629015.png" /> and any morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629016.png" /> of the generic fibres there exists a unique morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629017.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629018.png" />-schemes induced by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629019.png" />. |
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629020.png" /> is a one-dimensional regular Noetherian scheme, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629021.png" /> is a generic point of it, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629022.png" /> is its canonical imbedding, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629023.png" /> is an Abelian variety over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629024.png" />, then a Néron model of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629025.png" /> is defined as a smooth quasi-projective group scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629026.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629027.png" /> that represents the sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629028.png" /> relative to the flat Grothendieck topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629029.png" /> (see [[#References|[4]]]). | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629020.png" /> is a one-dimensional regular Noetherian scheme, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629021.png" /> is a generic point of it, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629022.png" /> is its canonical imbedding, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629023.png" /> is an Abelian variety over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629024.png" />, then a Néron model of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629025.png" /> is defined as a smooth quasi-projective group scheme <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629026.png" /> over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629027.png" /> that represents the sheaf <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629028.png" /> relative to the flat Grothendieck topology on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066290/n06629029.png" /> (see [[#References|[4]]]). | ||
Revision as of 20:53, 28 November 2014
of an Abelian variety
A group scheme associated to an Abelian variety and having a certain minimality property. If 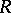 is a local Henselian discrete valuation ring with residue field
is a local Henselian discrete valuation ring with residue field 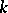 and field of fractions
and field of fractions 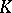 and if
and if  is an Abelian variety of dimension
is an Abelian variety of dimension 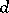 over
over 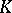 , then a Néron model of
, then a Néron model of  is defined as a smooth commutative group scheme
is defined as a smooth commutative group scheme 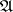 over
over 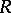 whose generic fibre
whose generic fibre 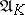 is isomorphic to
is isomorphic to 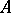 , while the canonical homomorphism
, while the canonical homomorphism 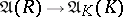 is an isomorphism. This concept was introduced by A. Néron [1] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an
is an isomorphism. This concept was introduced by A. Néron [1] in the case of a perfect field. In the local case a Néron model exists and is uniquely determined up to an 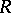 -isomorphism. A Néron model has the following minimality property: For any smooth
-isomorphism. A Néron model has the following minimality property: For any smooth 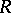 -scheme
-scheme 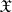 and any morphism
and any morphism  of the generic fibres there exists a unique morphism
of the generic fibres there exists a unique morphism 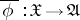 of
of  -schemes induced by
-schemes induced by 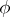 .
.
If 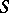 is a one-dimensional regular Noetherian scheme,
is a one-dimensional regular Noetherian scheme, 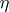 is a generic point of it,
is a generic point of it, 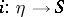 is its canonical imbedding, and
is its canonical imbedding, and  is an Abelian variety over
is an Abelian variety over 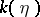 , then a Néron model of
, then a Néron model of 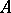 is defined as a smooth quasi-projective group scheme
is defined as a smooth quasi-projective group scheme 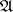 over
over 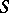 that represents the sheaf
that represents the sheaf 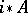 relative to the flat Grothendieck topology on
relative to the flat Grothendieck topology on 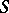 (see [4]).
(see [4]).
For a generalization of the concept of a Néron model to arbitrary schemes see [3].
References
| [1] | A. Néron, "Modèles minimaux des variétés abéliennes sur les corps locaux et globaux" Publ. Math. IHES , 21 (1964) |
| [2] | B. Mazur, "Rational points of Abelian varieties with values in towers of number fields" Invent. Math. , 18 (1974) pp. 183–266 |
| [3] | M. Raynaud, "Modèles de Néron" C.R. Acad. Sci. Paris Sér. A , 262 (1966) pp. 345–347 |
| [4] | M. Raynaud, "Caractéristique d'Euler–Poincaré d'un faisceau et cohomologie des variétés abéliennes (d'après Ogg–Shafarévitch et Grothendieck)" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 12–30 |
| [5] | A. Grothendieck (ed.) et al. (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7 , Lect. notes in math. , 288 , Springer (1972) |
Comments
References
| [a1] | M. Artin, "Néron models" G. Cornell (ed.) J. Silverman (ed.) , Arithmetic geometry , Springer (1986) pp. 213–230 |
Néron model. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=N%C3%A9ron_model&oldid=23428