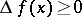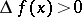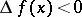Difference between revisions of "Monotone function"
m (ce) |
(related concepts) |
||
| Line 26: | Line 26: | ||
A monotone function of many variables, increasing or decreasing at some point, is defined as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483016.png" /> be defined on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483017.png" />-dimensional closed cube <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483018.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483019.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483020.png" /> be a [[Level set|level set]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483021.png" />. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483022.png" /> is called increasing (respectively, decreasing) at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483023.png" /> if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483024.png" /> and any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483025.png" /> not separated in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483026.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483027.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483028.png" />, the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483029.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483030.png" />) holds, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483031.png" /> that is separated in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483032.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483033.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483034.png" />, the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483035.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483036.png" />) holds. A function that is increasing or decreasing at some point is called monotone at that point. | A monotone function of many variables, increasing or decreasing at some point, is defined as follows. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483016.png" /> be defined on the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483017.png" />-dimensional closed cube <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483018.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483019.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483020.png" /> be a [[Level set|level set]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483021.png" />. The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483022.png" /> is called increasing (respectively, decreasing) at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483023.png" /> if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483024.png" /> and any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483025.png" /> not separated in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483026.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483027.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483028.png" />, the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483029.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483030.png" />) holds, and for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483031.png" /> that is separated in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483032.png" /> by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483033.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483034.png" />, the relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483035.png" /> (respectively, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064830/m06483036.png" />) holds. A function that is increasing or decreasing at some point is called monotone at that point. | ||
| + | |||
| + | ====Comments==== | ||
| + | For the concept in [[non-linear functional analysis]], see [[Monotone operator]]. For the concept in general [[partially ordered set]]s, see [[Monotone mapping]]. | ||
Revision as of 18:22, 15 November 2014
A function of one variable, defined on a subset of the real numbers, whose increment 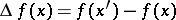 , for
, for 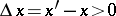 , does not change sign, that is, is either always negative or always positive. If
, does not change sign, that is, is either always negative or always positive. If 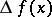 is strictly greater (less) than zero when
is strictly greater (less) than zero when  , then the function is called strictly monotone (see Increasing function; Decreasing function). The various types of monotone functions are represented in the following table.
, then the function is called strictly monotone (see Increasing function; Decreasing function). The various types of monotone functions are represented in the following table.
<tbody> </tbody>
|
If at each point of an interval 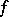 has a derivative that does not change sign (respectively, is of constant sign), then
has a derivative that does not change sign (respectively, is of constant sign), then 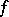 is monotone (strictly monotone) on this interval.
is monotone (strictly monotone) on this interval.
The idea of a monotone function can be generalized to functions of various classes. For example, a function 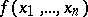 defined on
defined on 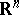 is called monotone if the condition
is called monotone if the condition 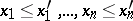 implies that everywhere either
implies that everywhere either 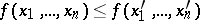 or
or 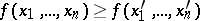 everywhere. A monotone function in the algebra of logic is defined similarly.
everywhere. A monotone function in the algebra of logic is defined similarly.
A monotone function of many variables, increasing or decreasing at some point, is defined as follows. Let 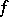 be defined on the
be defined on the  -dimensional closed cube
-dimensional closed cube 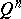 , let
, let 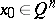 and let
and let 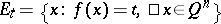 be a level set of
be a level set of 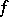 . The function
. The function 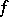 is called increasing (respectively, decreasing) at
is called increasing (respectively, decreasing) at 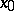 if for any
if for any  and any
and any 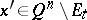 not separated in
not separated in 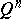 by
by 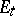 from
from 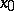 , the relation
, the relation 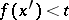 (respectively,
(respectively, 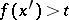 ) holds, and for any
) holds, and for any  that is separated in
that is separated in 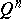 by
by 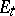 from
from 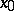 , the relation
, the relation 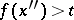 (respectively,
(respectively, 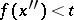 ) holds. A function that is increasing or decreasing at some point is called monotone at that point.
) holds. A function that is increasing or decreasing at some point is called monotone at that point.
Comments
For the concept in non-linear functional analysis, see Monotone operator. For the concept in general partially ordered sets, see Monotone mapping.
Monotone function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Monotone_function&oldid=34524