Difference between revisions of "Gamma-distribution"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
|||
| Line 23: | Line 23: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330021.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330021.png" /></td> </tr></table> | ||
| − | Gamma-distributions play a significant, though not always an explicit, role in applications. In the particular case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330022.png" /> one obtains the exponential density. In queueing theory, the gamma-distribution for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330023.png" /> which assumes integer values is known as the [[Erlang distribution|Erlang distribution]]. In mathematical statistics gamma-distributions frequently occur owing to the close connection with the normal distribution, since the sum of the squares <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330024.png" /> of independent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330025.png" /> normally-distributed random variables has density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330026.png" /> and is known as the "chi-squared" distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330027.png" /> degrees of freedom. For this reason the gamma-distribution is involved in many important distributions in problems of mathematical statistics dealing with quadratic forms of normally-distributed random variables (e.g. the [[Student distribution|Student distribution]], the [[Fisher-F-distribution|Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330028.png" />-distribution]] and the [[Fisher | + | Gamma-distributions play a significant, though not always an explicit, role in applications. In the particular case of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330022.png" /> one obtains the exponential density. In queueing theory, the gamma-distribution for an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330023.png" /> which assumes integer values is known as the [[Erlang distribution|Erlang distribution]]. In mathematical statistics gamma-distributions frequently occur owing to the close connection with the normal distribution, since the sum of the squares <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330024.png" /> of independent <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330025.png" /> normally-distributed random variables has density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330026.png" /> and is known as the "chi-squared" distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330027.png" /> degrees of freedom. For this reason the gamma-distribution is involved in many important distributions in problems of mathematical statistics dealing with quadratic forms of normally-distributed random variables (e.g. the [[Student distribution|Student distribution]], the [[Fisher-F-distribution|Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330028.png" />-distribution]] and the [[Fisher z-distribution|Fisher <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330029.png" />-distribution]]). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330030.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330031.png" /> are independent and are distributed with densities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330033.png" />, then the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330034.png" /> has density |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330035.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043300/g04330035.png" /></td> </tr></table> | ||
Revision as of 08:27, 19 October 2014
A continuous probability distribution concentrated on the positive semi-axis  with density
with density
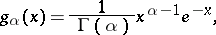 |
where  is a parameter assuming positive values, and
is a parameter assuming positive values, and  is Euler's gamma-function:
is Euler's gamma-function:
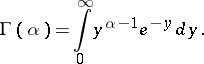 |
The corresponding distribution function for  is zero, and for
is zero, and for  it is expressed by the formula
it is expressed by the formula
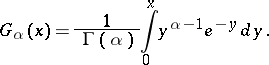 |
The integral on the right-hand side is called the incomplete gamma-function. The density  is unimodal and for
is unimodal and for 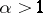 it attains the maximum
it attains the maximum 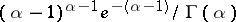 at the point
at the point 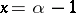 . If
. If  the density
the density 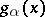 decreases monotonically with increasing
decreases monotonically with increasing  , and if
, and if 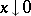 ,
, 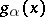 increases without limit. The characteristic function of the gamma-distribution has the form
increases without limit. The characteristic function of the gamma-distribution has the form
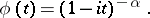 |
The moments of the gamma-distribution are given by the formula
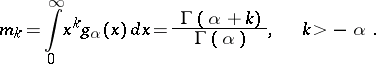 |
In particular, the mathematical expectation and variance are equal to 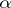 . The set of gamma-distributions is closed with respect to the operation of convolution:
. The set of gamma-distributions is closed with respect to the operation of convolution:
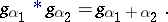 |
Gamma-distributions play a significant, though not always an explicit, role in applications. In the particular case of  one obtains the exponential density. In queueing theory, the gamma-distribution for an
one obtains the exponential density. In queueing theory, the gamma-distribution for an 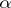 which assumes integer values is known as the Erlang distribution. In mathematical statistics gamma-distributions frequently occur owing to the close connection with the normal distribution, since the sum of the squares
which assumes integer values is known as the Erlang distribution. In mathematical statistics gamma-distributions frequently occur owing to the close connection with the normal distribution, since the sum of the squares 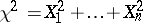 of independent
of independent 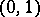 normally-distributed random variables has density
normally-distributed random variables has density  and is known as the "chi-squared" distribution with
and is known as the "chi-squared" distribution with  degrees of freedom. For this reason the gamma-distribution is involved in many important distributions in problems of mathematical statistics dealing with quadratic forms of normally-distributed random variables (e.g. the Student distribution, the Fisher
degrees of freedom. For this reason the gamma-distribution is involved in many important distributions in problems of mathematical statistics dealing with quadratic forms of normally-distributed random variables (e.g. the Student distribution, the Fisher 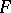 -distribution and the Fisher
-distribution and the Fisher  -distribution). If
-distribution). If  and
and 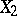 are independent and are distributed with densities
are independent and are distributed with densities  and
and 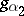 , then the random variable
, then the random variable 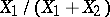 has density
has density
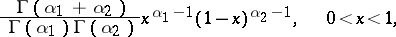 |
which is known as the density of the beta-distribution. The densities of linear functions 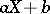 of random variables
of random variables  obeying the gamma-distribution constitute a special class of distributions — the so-called "type III" family of Pearson distributions. The density of the gamma-distribution is the weight function of the system of orthogonal Laguerre polynomials. The values of the gamma-distribution may be calculated from tables of the incomplete gamma-function [1], [2].
obeying the gamma-distribution constitute a special class of distributions — the so-called "type III" family of Pearson distributions. The density of the gamma-distribution is the weight function of the system of orthogonal Laguerre polynomials. The values of the gamma-distribution may be calculated from tables of the incomplete gamma-function [1], [2].
References
| [1] | V.I. Pagurova, "Tables of the incomplete gamma-function" , Moscow (1963) (In Russian) MR0159040 |
| [2] | K. Pearson (ed.) , Tables of the incomplete gamma function , Cambridge Univ. Press (1957) |
Comments
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics" , 1. Continuous univariate distributions , Wiley (1970) MR0270476 MR0270475 Zbl 0213.21101 |
| [a2] | L.J. Comrie, "Chambers's six-figure mathematical tables" , II , Chambers (1949) |
Gamma-distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gamma-distribution&oldid=24074