Difference between revisions of "Tangent, curve of the"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | The graph of the function | + | {{TEX|done}} |
| + | The graph of the function $g=\tan x$ (Fig.a). The curve of the [[Tangent|tangent]] is a periodic curve with period $T=\pi$ and asymptotes $x=(k+1/2)\pi$, $k\in\mathbf Z$. While $x$ varies from $-\pi/2$ to $+\pi/2$, $y$ grows monotonically from $-\infty$ to $+\infty$; thus, the curve of the tangent is composed of infinitely many separate congruent curves obtained from one another by translation over $k\pi$ along the $x$-axis. The points of intersection with the $x$-axis are $(k\pi,0)$. These are also the points of inflection, with inclination angle $\pi/4$ to the $x$-axis. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092130a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092130a.gif" /> | ||
| Line 5: | Line 6: | ||
Figure: t092130a | Figure: t092130a | ||
| − | The curve of the tangent reflected mirror-like in the | + | The curve of the tangent reflected mirror-like in the $x$-axis and translated to the left over $\pi/2$ (Fig.b) becomes the graph of the function $y=\operatorname{cotan}x=-\tan(\pi/2+x)$ (cf. [[Cotangent|Cotangent]]); its asymptotes are $x=k\pi$; its intersections with the $x$-axis are $((k+1/2)\pi,0)$ and these points are also the points of inflection, with inclination angle $\pi/4$ with respect to the $x$-axis. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092130b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/t092130b.gif" /> | ||
Figure: t092130b | Figure: t092130b | ||
Latest revision as of 18:15, 18 September 2014
The graph of the function $g=\tan x$ (Fig.a). The curve of the tangent is a periodic curve with period $T=\pi$ and asymptotes $x=(k+1/2)\pi$, $k\in\mathbf Z$. While $x$ varies from $-\pi/2$ to $+\pi/2$, $y$ grows monotonically from $-\infty$ to $+\infty$; thus, the curve of the tangent is composed of infinitely many separate congruent curves obtained from one another by translation over $k\pi$ along the $x$-axis. The points of intersection with the $x$-axis are $(k\pi,0)$. These are also the points of inflection, with inclination angle $\pi/4$ to the $x$-axis.
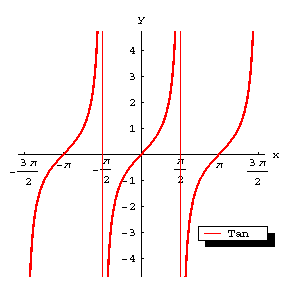
Figure: t092130a
The curve of the tangent reflected mirror-like in the $x$-axis and translated to the left over $\pi/2$ (Fig.b) becomes the graph of the function $y=\operatorname{cotan}x=-\tan(\pi/2+x)$ (cf. Cotangent); its asymptotes are $x=k\pi$; its intersections with the $x$-axis are $((k+1/2)\pi,0)$ and these points are also the points of inflection, with inclination angle $\pi/4$ with respect to the $x$-axis.
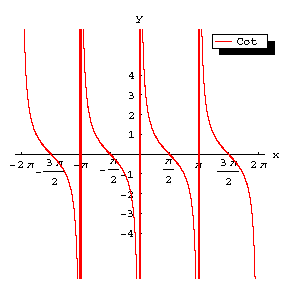
Figure: t092130b
How to Cite This Entry:
Tangent, curve of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent,_curve_of_the&oldid=11859
Tangent, curve of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent,_curve_of_the&oldid=11859
This article was adapted from an original article by Yu.A. Gor'kov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article