Difference between revisions of "Discriminant curve"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | ''of an ordinary first-order differential equation | + | {{TEX|done}} |
| + | ''of an ordinary first-order differential equation $F(x,y,y')=0$'' | ||
| − | The set of points | + | The set of points $(x,y)$ of the plane whose coordinates satisfy the equation $\phi(x,y)=0$ obtained by the elimination of $y'$ from the relations $F=0$ and $F_{y'}'=0$ or by elimination of $x'$ from the relations $G=0$ and $G_{y'}'=0$, where $G(y,x,x')\equiv F(x,y,1/x')$ (on the assumption that $F_{y'}'$ in fact exists). If the discriminant curve for the equation $F=0$ is a non-empty set and does not degenerate into individual points, the curve (or each one of its branches) may: |
| − | 1) be a solution of the equation | + | 1) be a solution of the equation $F=0$ at each point of which uniqueness is violated; the discriminant curve will then form the envelope of a family of integral curves (e.g. $y=1$ and $y=-1$ for the equation $y'^2+y^2-1=0$ (Fig. a); or $y=0$ for the equation $y'^3-y^2=0$ (Fig. b)); |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220a.gif" /> | ||
| Line 13: | Line 14: | ||
Figure: d033220b | Figure: d033220b | ||
| − | 2) be a solution of the equation | + | 2) be a solution of the equation $F=0$ at each point of which there is uniqueness (e.g. $y=0$ for the equation $y'^2-y^2=0$ (Fig. c)); |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220c.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220c.gif" /> | ||
| Line 19: | Line 20: | ||
Figure: d033220c | Figure: d033220c | ||
| − | 3) not be a solution of the equation | + | 3) not be a solution of the equation $F=0$. In this case the discriminant curve is either the set of cuspidal points of the integral curves (e.g. $x=0$ for the equation $y'^2-x=0$ (Fig. d)) or the set of osculation points of different integral curves (e.g. $x=0$ for the equation $y'^2-x^2=0$ (Fig. e)). |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220d.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/d033220d.gif" /> | ||
| Line 29: | Line 30: | ||
Figure: d033220e | Figure: d033220e | ||
| − | The equation | + | The equation $F=0$, when $F$ is a polynomial in $y'$, is also studied in the complex domain [[#References|[2]]]. |
====References==== | ====References==== | ||
Revision as of 13:54, 10 August 2014
of an ordinary first-order differential equation $F(x,y,y')=0$
The set of points $(x,y)$ of the plane whose coordinates satisfy the equation $\phi(x,y)=0$ obtained by the elimination of $y'$ from the relations $F=0$ and $F_{y'}'=0$ or by elimination of $x'$ from the relations $G=0$ and $G_{y'}'=0$, where $G(y,x,x')\equiv F(x,y,1/x')$ (on the assumption that $F_{y'}'$ in fact exists). If the discriminant curve for the equation $F=0$ is a non-empty set and does not degenerate into individual points, the curve (or each one of its branches) may:
1) be a solution of the equation $F=0$ at each point of which uniqueness is violated; the discriminant curve will then form the envelope of a family of integral curves (e.g. $y=1$ and $y=-1$ for the equation $y'^2+y^2-1=0$ (Fig. a); or $y=0$ for the equation $y'^3-y^2=0$ (Fig. b));
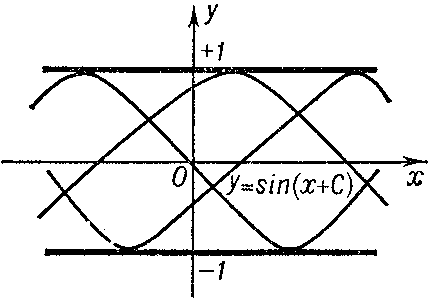
Figure: d033220a
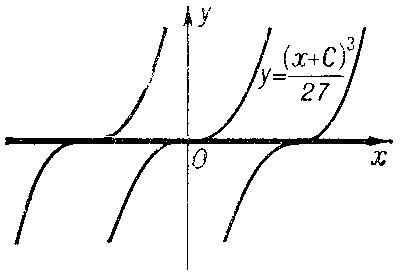
Figure: d033220b
2) be a solution of the equation $F=0$ at each point of which there is uniqueness (e.g. $y=0$ for the equation $y'^2-y^2=0$ (Fig. c));
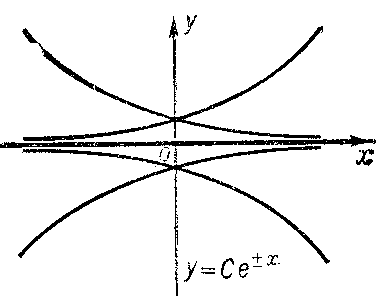
Figure: d033220c
3) not be a solution of the equation $F=0$. In this case the discriminant curve is either the set of cuspidal points of the integral curves (e.g. $x=0$ for the equation $y'^2-x=0$ (Fig. d)) or the set of osculation points of different integral curves (e.g. $x=0$ for the equation $y'^2-x^2=0$ (Fig. e)).
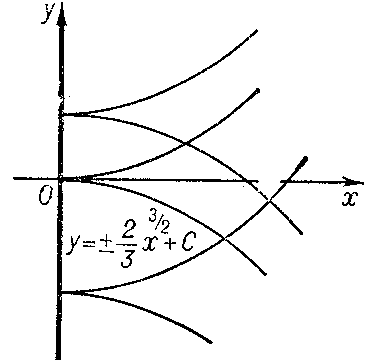
Figure: d033220d
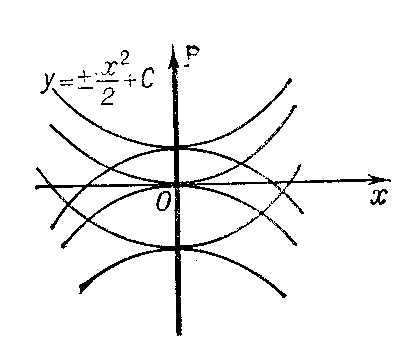
Figure: d033220e
The equation $F=0$, when $F$ is a polynomial in $y'$, is also studied in the complex domain [2].
References
| [1] | G. Sansone, "Equazioni differenziali nel campo reale" , 2 , Zanichelli (1949) |
| [2] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
Comments
References
| [a1] | E.L. Ince, "Ordinary differential equations" , Dover, reprint (1956) |
Discriminant curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Discriminant_curve&oldid=15781