Difference between revisions of "Hyperbolic spiral"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A plane transcendental curve whose equation in polar coordinates is | A plane transcendental curve whose equation in polar coordinates is | ||
| − | + | $$\rho=\frac a\phi.$$ | |
| − | It consists of two branches, which are symmetric with respect to a straight line | + | It consists of two branches, which are symmetric with respect to a straight line $d$ (see Fig.). The pole is an asymptotic point. The asymptote is the straight line parallel to the polar axis at a distance $a$ from it. The arc length between two points $M_1(\rho_1,\phi_1)$ and $M_2(\rho_2,\phi_2)$ is |
| − | + | $$l=a\left[-\frac{\sqrt{1+\phi^2}}{\phi}+\ln(\phi+\sqrt{1+\phi^2})\right]_{\phi_1}^{\phi_2}.$$ | |
| − | The area of the sector bounded by an arc of the hyperbolic spiral and the two radius vectors | + | The area of the sector bounded by an arc of the hyperbolic spiral and the two radius vectors $\rho_1$ and $\rho_2$ corresponding to the angles $\phi_1$ and $\phi_2$ is |
| − | + | $$S=\frac{a^2(\rho_1-\rho_2}{2}.$$ | |
| − | A hyperbolic spiral and an [[Archimedean spiral|Archimedean spiral]] may be obtained from each other by inversion with respect to the pole | + | A hyperbolic spiral and an [[Archimedean spiral|Archimedean spiral]] may be obtained from each other by inversion with respect to the pole $O$ of the hyperbolic spiral. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h048340a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/h048340a.gif" /> | ||
Revision as of 11:47, 26 July 2014
A plane transcendental curve whose equation in polar coordinates is
$$\rho=\frac a\phi.$$
It consists of two branches, which are symmetric with respect to a straight line $d$ (see Fig.). The pole is an asymptotic point. The asymptote is the straight line parallel to the polar axis at a distance $a$ from it. The arc length between two points $M_1(\rho_1,\phi_1)$ and $M_2(\rho_2,\phi_2)$ is
$$l=a\left[-\frac{\sqrt{1+\phi^2}}{\phi}+\ln(\phi+\sqrt{1+\phi^2})\right]_{\phi_1}^{\phi_2}.$$
The area of the sector bounded by an arc of the hyperbolic spiral and the two radius vectors $\rho_1$ and $\rho_2$ corresponding to the angles $\phi_1$ and $\phi_2$ is
$$S=\frac{a^2(\rho_1-\rho_2}{2}.$$
A hyperbolic spiral and an Archimedean spiral may be obtained from each other by inversion with respect to the pole $O$ of the hyperbolic spiral.
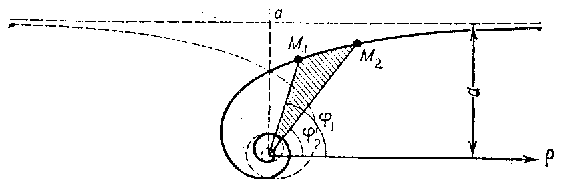
Figure: h048340a
A hyperbolic spiral is a special case of the so-called algebraic spirals.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Hyperbolic spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hyperbolic_spiral&oldid=12776