Difference between revisions of "Fermat spiral"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A planar transcendental curve the equation of which in polar coordinates has the form | A planar transcendental curve the equation of which in polar coordinates has the form | ||
| − | + | $$\rho=a\sqrt\phi.$$ | |
| − | To each value of | + | To each value of $\phi$ correspond two values of $\rho$ — a positive and a negative one. The Fermat spiral is centrally symmetric relative to the pole, which is a point of inflection. It belongs to the class of so-called algebraic [[Spirals|spirals]]. |
They were first studied by P. Fermat (1636). | They were first studied by P. Fermat (1636). | ||
Revision as of 11:13, 26 July 2014
A planar transcendental curve the equation of which in polar coordinates has the form
$$\rho=a\sqrt\phi.$$
To each value of $\phi$ correspond two values of $\rho$ — a positive and a negative one. The Fermat spiral is centrally symmetric relative to the pole, which is a point of inflection. It belongs to the class of so-called algebraic spirals.
They were first studied by P. Fermat (1636).
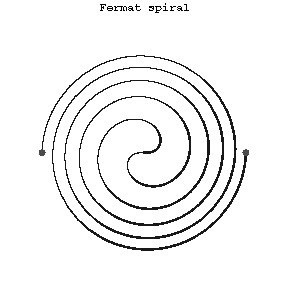
Figure: f038420a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
How to Cite This Entry:
Fermat spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat_spiral&oldid=15613
Fermat spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fermat_spiral&oldid=15613
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article