Difference between revisions of "Witch of Agnesi"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''versiera'' | ''versiera'' | ||
A plane curve, given in the Cartesian orthogonal coordinate system by the equation | A plane curve, given in the Cartesian orthogonal coordinate system by the equation | ||
| − | + | $$y(a^2+x^2)=a^3,\quad a>0.$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w098050a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/w098050a.gif" /> | ||
| Line 9: | Line 10: | ||
Figure: w098050a | Figure: w098050a | ||
| − | If | + | If $a$ is the diameter of a circle with centre at the point $(0,a/2)$, $OA$ is a secant, $CB$ and $AM$ are parallel to the $x$-axis, and $BM$ is parallel to the $y$-axis (see Fig.), then the witch of Agnesi is the locus of the points $M$. If the centre of the generating circle and the tangent $CB$ are shifted along the $y$-axis, the curve thus obtained is called Newton's aguinea and is a generalization of the witch of Agnesi. The curve is named after M. Agnesi (1748), who studied it. |
====References==== | ====References==== | ||
Revision as of 14:05, 21 June 2014
versiera
A plane curve, given in the Cartesian orthogonal coordinate system by the equation
$$y(a^2+x^2)=a^3,\quad a>0.$$
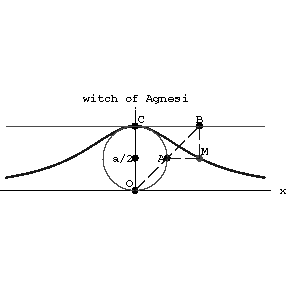
Figure: w098050a
If $a$ is the diameter of a circle with centre at the point $(0,a/2)$, $OA$ is a secant, $CB$ and $AM$ are parallel to the $x$-axis, and $BM$ is parallel to the $y$-axis (see Fig.), then the witch of Agnesi is the locus of the points $M$. If the centre of the generating circle and the tangent $CB$ are shifted along the $y$-axis, the curve thus obtained is called Newton's aguinea and is a generalization of the witch of Agnesi. The curve is named after M. Agnesi (1748), who studied it.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
How to Cite This Entry:
Witch of Agnesi. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witch_of_Agnesi&oldid=18586
Witch of Agnesi. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witch_of_Agnesi&oldid=18586
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article