Difference between revisions of "Cissoid"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A plane algebraic curve of order three whose equation in Cartesian coordinates is | A plane algebraic curve of order three whose equation in Cartesian coordinates is | ||
| − | + | $$y^2=\frac{x^3}{2a-x}.$$ | |
The parametric equations are | The parametric equations are | ||
| − | + | $$x=\frac{2at^2}{t^2+1},\quad y=\frac{2at^3}{t^2+1}.$$ | |
| − | A cissoid is symmetric relative to the | + | A cissoid is symmetric relative to the $x$-axis (Fig.). The coordinate origin is a cusp, the asymptote is $x=2a$. The area between the curve and the asymptote is $S=3\pi a^2$. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c022340a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/c022340a.gif" /> | ||
| Line 15: | Line 16: | ||
The cissoid is often called the cissoid of Diocles in honour of the Ancient Greek mathematician Diocles (3rd century B.C.), who discussed it in connection with the problem of [[Duplication of the cube|duplication of the cube]]. | The cissoid is often called the cissoid of Diocles in honour of the Ancient Greek mathematician Diocles (3rd century B.C.), who discussed it in connection with the problem of [[Duplication of the cube|duplication of the cube]]. | ||
| − | The cissoid is the set of points | + | The cissoid is the set of points $M$ for which $OM=CB$, where $B$ and $C$ are the points of intersection of the line $OM$ with a circle and the tangent $AB$ to the circle at the point $A$ diametrically opposite to $O$. If in this construction one replaces the circle and straight line by curves $\rho_1=f_1(\phi)$ and $\rho_2=f_2(\phi)$, then the resulting curve $\rho=\rho_1-\rho_2$ is called a cissoidal curve, or the cissoid of the (given) curves. |
====References==== | ====References==== | ||
Revision as of 13:48, 25 April 2014
A plane algebraic curve of order three whose equation in Cartesian coordinates is
$$y^2=\frac{x^3}{2a-x}.$$
The parametric equations are
$$x=\frac{2at^2}{t^2+1},\quad y=\frac{2at^3}{t^2+1}.$$
A cissoid is symmetric relative to the $x$-axis (Fig.). The coordinate origin is a cusp, the asymptote is $x=2a$. The area between the curve and the asymptote is $S=3\pi a^2$.
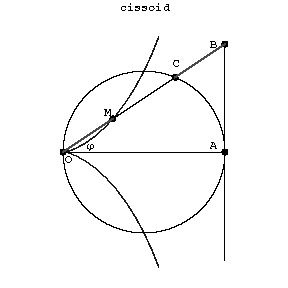
Figure: c022340a
The cissoid is often called the cissoid of Diocles in honour of the Ancient Greek mathematician Diocles (3rd century B.C.), who discussed it in connection with the problem of duplication of the cube.
The cissoid is the set of points $M$ for which $OM=CB$, where $B$ and $C$ are the points of intersection of the line $OM$ with a circle and the tangent $AB$ to the circle at the point $A$ diametrically opposite to $O$. If in this construction one replaces the circle and straight line by curves $\rho_1=f_1(\phi)$ and $\rho_2=f_2(\phi)$, then the resulting curve $\rho=\rho_1-\rho_2$ is called a cissoidal curve, or the cissoid of the (given) curves.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
Comments
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) |
| [a2] | E. Brieskorn, H. Knörrer, "Ebene algebraische Kurven" , Birkhäuser (1981) |
How to Cite This Entry:
Cissoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cissoid&oldid=18260
Cissoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cissoid&oldid=18260
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article