Difference between revisions of "Banaschewski compactification"
(Importing text file) |
m (link) |
||
| Line 1: | Line 1: | ||
| − | A [[Topological space|topological space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101201.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101203.png" />-dimensional if it is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101204.png" />-space (cf. also [[Separation axiom|Separation axiom]]) with a base of clopen sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [[#References|[a1]]], [[#References|[a2]]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101205.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101206.png" />, is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101207.png" />-dimensional analogue of the [[Stone–Čech compactification|Stone–Čech compactification]] of a [[Tikhonov space|Tikhonov space]]. It can be obtained as the [[Stone space|Stone space]] of the [[Boolean algebra|Boolean algebra]] of clopen subsets. | + | A [[Topological space|topological space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101201.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101203.png" />-dimensional if it is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101204.png" />-space (cf. also [[Separation axiom|Separation axiom]]) with a base of [[clopen]] sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [[#References|[a1]]], [[#References|[a2]]] of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101205.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101206.png" />, is the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b110/b110120/b1101207.png" />-dimensional analogue of the [[Stone–Čech compactification|Stone–Čech compactification]] of a [[Tikhonov space|Tikhonov space]]. It can be obtained as the [[Stone space|Stone space]] of the [[Boolean algebra|Boolean algebra]] of clopen subsets. |
The Banaschewski compactification is also a special case of the [[Wallman compactification|Wallman compactification]] [[#References|[a4]]] (as generalized by N.A. Shanin, [[#References|[a3]]]). A fairly general approach subsuming the above-mentioned compactifications is as follows. | The Banaschewski compactification is also a special case of the [[Wallman compactification|Wallman compactification]] [[#References|[a4]]] (as generalized by N.A. Shanin, [[#References|[a3]]]). A fairly general approach subsuming the above-mentioned compactifications is as follows. | ||
Revision as of 18:35, 30 September 2013
A topological space 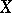 is
is  -dimensional if it is a
-dimensional if it is a 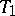 -space (cf. also Separation axiom) with a base of clopen sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [a1], [a2] of
-space (cf. also Separation axiom) with a base of clopen sets (a set is called clopen if it is both open and closed). The Banaschewski compactification [a1], [a2] of 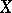 , denoted by
, denoted by 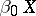 , is the
, is the  -dimensional analogue of the Stone–Čech compactification of a Tikhonov space. It can be obtained as the Stone space of the Boolean algebra of clopen subsets.
-dimensional analogue of the Stone–Čech compactification of a Tikhonov space. It can be obtained as the Stone space of the Boolean algebra of clopen subsets.
The Banaschewski compactification is also a special case of the Wallman compactification [a4] (as generalized by N.A. Shanin, [a3]). A fairly general approach subsuming the above-mentioned compactifications is as follows.
Let 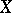 be an arbitrary non-empty set and
be an arbitrary non-empty set and 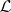 a lattice of subsets of
a lattice of subsets of 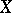 such that
such that 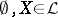 . Assume that
. Assume that 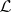 is disjunctive and separating, let
is disjunctive and separating, let 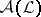 be the algebra generated by
be the algebra generated by 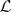 , let
, let 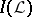 be the set of non-trivial zero-one valued finitely additive measures on
be the set of non-trivial zero-one valued finitely additive measures on 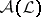 , and let
, and let 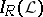 be the set of elements
be the set of elements 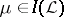 that are
that are 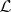 -regular, i.e.,
-regular, i.e.,
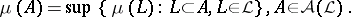 |
One can identify 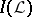 with the
with the 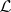 -prime filters and
-prime filters and 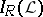 with the
with the 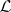 -ultrafilters (cf. also Filter; Ultrafilter).
-ultrafilters (cf. also Filter; Ultrafilter).
Next, let 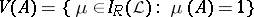 , where
, where 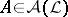 ;
; 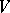 is a lattice isomorphism from
is a lattice isomorphism from 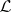 to
to 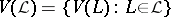 . Take
. Take 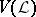 as a base for the closed sets of a topology
as a base for the closed sets of a topology 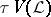 on
on 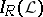 . Then
. Then 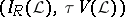 is a compact
is a compact 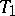 -space and it is
-space and it is 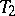 (cf. Hausdorff space) if and only if
(cf. Hausdorff space) if and only if 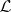 is a normal lattice.
is a normal lattice. 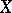 can be densely imbedded in
can be densely imbedded in 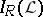 by the mapping
by the mapping 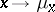 , where
, where 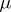 is the Dirac measure concentrated at
is the Dirac measure concentrated at  (cf. also Dirac delta-function). The mapping is a homeomorphism if
(cf. also Dirac delta-function). The mapping is a homeomorphism if 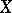 is given the topology of closed sets with
is given the topology of closed sets with 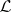 as base for the closed sets.
as base for the closed sets.
If 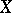 is a
is a 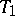 -space and
-space and 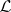 is the lattice of closed sets, then
is the lattice of closed sets, then 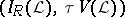 becomes the usual Wallman compactification
becomes the usual Wallman compactification 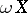 .
.
If 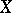 is a Tikhonov space and
is a Tikhonov space and 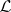 is the lattice of zero sets, then
is the lattice of zero sets, then 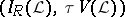 becomes the Stone–Čech compactification
becomes the Stone–Čech compactification 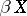 .
.
If 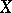 is a
is a  -dimensional
-dimensional 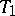 -space and
-space and 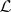 is the lattice of clopen sets, then
is the lattice of clopen sets, then 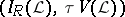 becomes the Banaschewski compactification
becomes the Banaschewski compactification 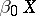 .
.
 if and only if
if and only if 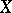 is a normal space;
is a normal space; 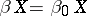 if and only if
if and only if 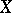 is strongly
is strongly  -dimensional (i.e., the clopen sets separate the zero sets).
-dimensional (i.e., the clopen sets separate the zero sets).
References
| [a1] | B. Banaschewski, "Über nulldimensional Räume" Math. Nachr. , 13 (1955) pp. 129–140 |
| [a2] | B. Banaschewski, "On Wallman's method of compactification" Math. Nachr. , 27 (1963) pp. 105–114 |
| [a3] | N.A. Shanin, "On the theory of bicompact extensions of topological spaces" Dokl. Aka. Nauk SSSR , 38 (1943) pp. 154–156 (In Russian) |
| [a4] | H. Wallman, "Lattices and topological spaces" Ann. Math. , 39 (1938) pp. 112–126 |
Banaschewski compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Banaschewski_compactification&oldid=15460