Difference between revisions of "Sieve method"
m (start conversion) |
(more conversion) |
||
| Line 1: | Line 1: | ||
A general method in number theory which generalizes the principle of sifting compound numbers from the natural series (see [[Eratosthenes, sieve of|Eratosthenes, sieve of]]). The problem of the sieve method consists in evaluating for a finite set $A$ of integers the quantity of those elements that are not divisible by any prime number $p$ from some set $P$ of prime numbers. The "sifting" function $S(A;P,x)$, which denotes the number of such elements from $A$ under the additional condition $p < x$, is often estimated by using information about the number $N(A_q)$ of elements of a set $A_q$. This set $A_q$ consists of the elements of $A$ that are divisible by a square-free number $q$. When $q=1$, $A_q = A$. Therefore the more general sifting function $S(A_q;P,x)$ is usually estimated. | A general method in number theory which generalizes the principle of sifting compound numbers from the natural series (see [[Eratosthenes, sieve of|Eratosthenes, sieve of]]). The problem of the sieve method consists in evaluating for a finite set $A$ of integers the quantity of those elements that are not divisible by any prime number $p$ from some set $P$ of prime numbers. The "sifting" function $S(A;P,x)$, which denotes the number of such elements from $A$ under the additional condition $p < x$, is often estimated by using information about the number $N(A_q)$ of elements of a set $A_q$. This set $A_q$ consists of the elements of $A$ that are divisible by a square-free number $q$. When $q=1$, $A_q = A$. Therefore the more general sifting function $S(A_q;P,x)$ is usually estimated. | ||
| − | The choice of an expected value for | + | The choice of an expected value for $N(A_q)$ in the form $\omega(q)/q)X$, where $X$ is the expected value for $N(A)$ and $\omega(\cdot)$ is a [[multiplicative function]], is governed by the fact that the magnitude of the error |
| + | $$ | ||
| + | R(X,q) = N(A_q) - \frac{\omega(q)}{q} X | ||
| + | $$ | ||
| + | should be relatively small. If, moreover, $\omega(q) = k$ (at least "on the average" ), then $k$ is called the dimension of the sieve. | ||
| − | + | The most advanced branch of the general theory of the sieve method and its applications is that of the linear sieve (when $k=1$). There are various specializations, the most important of which are the [[Brun sieve|Brun sieve]] and the [[Selberg sieve|Selberg sieve]]. | |
| − | |||
| − | |||
| − | |||
| − | The most advanced branch of the general theory of the sieve method and its applications is that of the linear sieve (when | ||
When the sieve method is applied to additive problems (see [[Additive number theory|Additive number theory]]), the sifting function must be estimated from below as well as from above. Estimates from below may be based on the logical combinatorial identity | When the sieve method is applied to additive problems (see [[Additive number theory|Additive number theory]]), the sifting function must be estimated from below as well as from above. Estimates from below may be based on the logical combinatorial identity | ||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> K. Prachar, "Primzahlverteilung" , Springer (1957)</TD></TR> | ||
| + | <TR><TD valign="top">[2]</TD> <TD valign="top"> A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974)</TD></TR> | ||
| + | </table> | ||
Revision as of 06:29, 28 August 2013
A general method in number theory which generalizes the principle of sifting compound numbers from the natural series (see Eratosthenes, sieve of). The problem of the sieve method consists in evaluating for a finite set $A$ of integers the quantity of those elements that are not divisible by any prime number $p$ from some set $P$ of prime numbers. The "sifting" function $S(A;P,x)$, which denotes the number of such elements from $A$ under the additional condition $p < x$, is often estimated by using information about the number $N(A_q)$ of elements of a set $A_q$. This set $A_q$ consists of the elements of $A$ that are divisible by a square-free number $q$. When $q=1$, $A_q = A$. Therefore the more general sifting function $S(A_q;P,x)$ is usually estimated.
The choice of an expected value for $N(A_q)$ in the form $\omega(q)/q)X$, where $X$ is the expected value for $N(A)$ and $\omega(\cdot)$ is a multiplicative function, is governed by the fact that the magnitude of the error $$ R(X,q) = N(A_q) - \frac{\omega(q)}{q} X $$ should be relatively small. If, moreover, $\omega(q) = k$ (at least "on the average" ), then $k$ is called the dimension of the sieve.
The most advanced branch of the general theory of the sieve method and its applications is that of the linear sieve (when $k=1$). There are various specializations, the most important of which are the Brun sieve and the Selberg sieve.
When the sieve method is applied to additive problems (see Additive number theory), the sifting function must be estimated from below as well as from above. Estimates from below may be based on the logical combinatorial identity
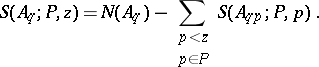 |
The most precise estimates from below are obtained by invoking combinatorial considerations associated with the use of weight functions. A strong result in the applications of the sieve method with weight functions is that each sufficiently large even number 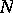 is representable in the form
is representable in the form 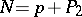 , where
, where 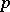 is a prime number and
is a prime number and 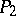 contains at most two prime factors.
contains at most two prime factors.
References
| [1] | K. Prachar, "Primzahlverteilung" , Springer (1957) |
| [2] | A.O. Gel'fond, Yu.V. Linnik, "Elementary methods in the analytic theory of numbers" , M.I.T. (1966) (Translated from Russian) |
| [3] | H. Halberstam, H.-E. Richert, "Sieve methods" , Acad. Press (1974) |
Comments
The first sieve method was known as Brun's sieve, after V. Brun, who proved in 1919 that 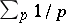 , where the sum is taken over all twin primes, converges. Using the sieve idea and some additional analytic tools, J. Chen proved in 1973 that there exist infinitely many primes
, where the sum is taken over all twin primes, converges. Using the sieve idea and some additional analytic tools, J. Chen proved in 1973 that there exist infinitely many primes 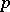 such that
such that 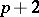 is a
is a 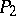 -number. (A
-number. (A 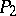 -number is a number which is either prime or the product of two primes.) By the same technique Chen proved that every number
-number is a number which is either prime or the product of two primes.) By the same technique Chen proved that every number 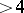 is the sum of a prime and a
is the sum of a prime and a 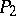 -number, thus coming very close to the solution of the Goldbach problem.
-number, thus coming very close to the solution of the Goldbach problem.
Based on totally different ideas is the large sieve invented by Yu.V. Linnik in 1941.
Sieve method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sieve_method&oldid=29597