Zeta-function method for regularization

zeta-function regularization

Regularization and renormalization procedures are essential issues in contemporary physics — without which it would simply not exist, at least in the form known today (2000). They are also essential in supersymmetry calculations. Among the different methods, zeta-function regularization — which is obtained by analytic continuation in the complex plane of the zeta-function of the relevant physical operator in each case — might well be the most beautiful of all. Use of this method yields, for instance, the vacuum energy corresponding to a quantum physical system (with constraints of any kind, in principle). Assuming the corresponding Hamiltonian operator, , has a spectral decomposition of the form (think, as simplest case, of a quantum harmonic oscillator): , with some set of indices (which can be discrete, continuous, mixed, multiple, etc.), then the quantum vacuum energy is obtained as follows [a5], [a6]:

where 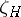is the zeta-function corresponding to the operator . The formal sum over the eigenvalues is usually ill-defined, and the last step involves analytic continuation, inherent to the definition of the zeta-function itself. These mathematically simple-looking relations involve very deep physical concepts (no wonder that understanding them took several decades in the recent history of quantum field theory, QFT). The zeta-function method is unchallenged at the one-loop level, where it is rigorously defined and where many calculations of QFT reduce basically (from a mathematical point of view) to the computation of determinants of elliptic pseudo-differential operators (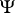DOs, cf. also Pseudo-differential operator) [a2]. It is thus no surprise that the preferred definition of determinant for such operators is obtained through the corresponding zeta-function.

When one comes to specific calculations, the zeta-function regularization method relies on the existence of simple formulas for obtaining the analytic continuation above. These consist of the reflection formula of the corresponding zeta-function in each case, together with some other fundamental expressions, as the Jacobi theta-function identity, Poisson's resummation formula and the famous Chowla–Selberg formula [a2]. However, some of these formulas are restricted to very specific zeta-functions, and it often turned out that for some physically important cases the corresponding formulas did not exist in the literature. This has required a painful process (it has taken over a decade already) of generalization of previous results and derivation of new expressions of this kind [a5], [a6]. [a1].

zeta regularization for integrals

The zeta function regularization may be have extended in order to include divergent integrals \begin{equation} \int_{a}^{\infty}x^{m}dx \qquad m >0 \end{equation} by using the recurrence equation

\begin{equation} \begin{array}{l} \int\nolimits_{a}^{\infty }x^{m-s} dx =\frac{m-s}{2} \int\nolimits_{a}^{\infty }x^{m-1-s} dx +\zeta (s-m)-\sum\limits_{i=1}^{a}i^{m-s} +a^{m-s} \\ -\sum\limits_{r=1}^{\infty }\frac{B_{2r} \Gamma (m-s+1)}{(2r)!\Gamma (m-2r+2-s)} (m-2r+1-s)\int\nolimits_{a}^{\infty }x^{m-2r-s} dx \end{array} \end{equation}

this is the natural extension to integrals of the Zeta regularization algorithm , this recurrence equation is finite since for \begin{equation} m-2r < -1 \qquad \int_{a}^{\infty}dxx^{m-2r}= -\frac{a^{m-2r+1}}{m-2r+1} \end{equation} the integrals inside the recurrence equation are convergents

References

[a1]	A.A. Bytsenko, G. Cognola, L. Vanzo, S. Zerbini, "Quantum fields and extended objects in space-times with constant curvature spatial section" Phys. Rept. , 266 (1996) pp. 1–126
[a2]	E. Elizalde, "Multidimensional extension of the generalized Chowla–Selberg formula" Commun. Math. Phys. , 198 (1998) pp. 83–95
[a3]	S.W. Hawking, "Zeta function regularization of path integrals in curved space time" Commun. Math. Phys. , 55 (1977) pp. 133–148
[a4]	M. Nakahara, "Geometry, topology, and physics" , Inst. Phys. (1995) pp. 7–8
[a5]	E. Elizalde, S.D. Odintsov, A. Romeo, A.A. Bytsenko, S. Zerbini, "Zeta regularization techniques with applications" , World Sci. (1994)
[a6]	E. Elizalde, "Ten physical applications of spectral zeta functions" , Springer (1995)