Carmichael number

A composite natural number for which 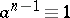modulo , whenever is relatively prime to . Thus they are pseudo-primes (cf. Pseudo-prime) for every such base . These numbers play a role in the theory of probabilistic primality tests (cf. Probabilistic primality test), as they show that Fermat's theorem, to wit $ a^p \equiv a $ modulo 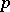, whenever 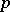is prime and 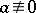modulo 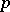, is not a sufficient criterion for primality (cf. also Fermat little theorem).

The first five Carmichael numbers are

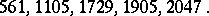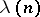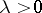R.D. Carmichael [a2] characterized them as follows. Let be the exponent of the multiplicative group of integers modulo , that is, the least making all 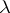th powers in the group equal to 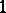. (This is readily computed from the prime factorization of .) Then a composite natural number is Carmichael if and only if 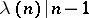. From this it follows that every Carmichael number is odd, square-free, and has at least distinct prime factors.

Let 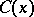denote the number of Carmichael numbers 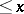. W.R. Alford, A. Granville and C. Pomerance [a1] proved that 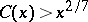for sufficiently large . This settled a long-standing conjecture that there are infinitely many Carmichael numbers. It is believed on probabilistic grounds that 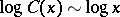[a4].

There is apparently no better way to compute 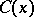than to make a list of the Carmichael numbers up to . The most exhaustive computation to date (1996) is that of R.G.E. Pinch, who used the methods of [a3] to determine that .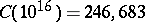

References

[a1]	W.R. Alford, A. Granville, C. Pomerance, "There are infinitely many Carmichael numbers" Ann. of Math. , 140 (1994) pp. 703–722
[a2]	R.D. Carmichael, "Note on a new number theory function" Bull. Amer. Math. Soc. , 16 (1910) pp. 232–238 (See also: Amer. Math. Monthly 19 (1912), 22–27)
[a3]	R.G.E. Pinch, "The Carmichael numbers up to 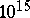" Math. Comp. , 61 (1993) pp. 381–391
[a4]	C. Pomerance, J.L. Selfridge, S.S. Wagstaff, Jr., "The pseudoprimes to 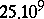" Math. Comp. , 35 (1980) pp. 1003–1026