Difference between revisions of "Schauder theorem"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (some Tex + link) |
||
| Line 1: | Line 1: | ||
| − | One of the [[Fixed point|fixed point]] theorems: If a completely-continuous operator | + | One of the [[Fixed point|fixed point]] theorems: If a [[Completely-continuous_operator|completely-continuous operator]] $A$ maps a bounded closed convex set $K$ of a Banach space $X$ into itself, then there exists at least one point $x\in K$ such that $Ax=x$. Proved by J. Schauder [[#References|[1]]] as a generalization of the [[Brouwer theorem|Brouwer theorem]]. |
There exist different generalizations of Schauder's theorem: the Markov–Kakutani theorem, Tikhonov's principle, etc. | There exist different generalizations of Schauder's theorem: the Markov–Kakutani theorem, Tikhonov's principle, etc. | ||
Revision as of 07:56, 14 December 2012
One of the fixed point theorems: If a completely-continuous operator $A$ maps a bounded closed convex set $K$ of a Banach space $X$ into itself, then there exists at least one point $x\in K$ such that $Ax=x$. Proved by J. Schauder [1] as a generalization of the Brouwer theorem.
There exist different generalizations of Schauder's theorem: the Markov–Kakutani theorem, Tikhonov's principle, etc.
References
| [1] | J. Schauder, "Der Fixpunktsatz in Funktionalräumen" Stud. Math. , 2 (1930) pp. 171–180 Zbl 56.0355.01 |
| [2] | L.A. Lyusternik, V.I. Sobolev, "Elements of functional analysis" , Hindushtan Publ. Comp. (1974) (Translated from Russian) MR0539144 MR0048693 Zbl 0141.11601 Zbl 0096.07802 |
| [3] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
| [4] | R.E. Edwards, "Functional analysis: theory and applications" , Holt, Rinehart & Winston (1965) MR0221256 Zbl 0182.16101 |
| [5] | L. Nirenberg, "Topics in nonlinear functional analysis" , New York Univ. Inst. Math. Mech. (1974) MR0488102 Zbl 0286.47037 |
Comments
The Tikhonov fixed-point theorem (also spelled Tychonoff's fixed-point theorem) states the following. Let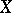 
be a locally convex topological space whose topology is defined by a family 
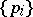of continuous semi-norms. Let 
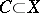be compact and convex and 
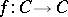a continuous mapping. Then 
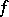has a fixed point in 
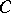([a2]; [a3], p. 175). Both the Kakutani fixed-point theorem and the Markov fixed-point theorem are generalized in the Ryll-Nardzewski fixed-point theorem, which states: Let 
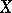be a Banach space and 
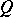a non-empty weakly compact subset. Let 
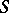be a semi-group of mappings from 
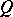to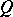 
which is non-contracting, then there is a fixed point of 
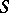. Here, a family 
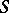of mappings is said to have a fixed point 
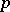if for every 
, 
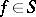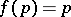, [a4]; cf. [a3], Chapt. 9, for a discussion of the Ryll-Nardzewski fixed-point theorem in relation to the Kakutani and Markov ones and other fixed-point theorems for families of mappings.
References
| [a1] | J. Dugundji, A. Granas, "Fixed-point theory" , I , PWN (1982) MR0660439 Zbl 0483.47038 |
| [a2] | A.N. [A.N. Tikhonov] Tychonoff, "Ein Fixpunktsatz" Math. Ann. , 111 (1935) pp. 767–776 MR1513031 Zbl 0012.30803 Zbl 61.1195.01 |
| [a3] | V.I. Istrăţescu, "Fixed point theory" , Reidel (1981) MR0620639 Zbl 0465.47035 |
| [a4] | C. Ryll-Nardzewski, "On fixed points of semi-groups of endomorphisms of linear spaces" , Proc. 5-th Berkeley Symp. Probab. Math. Stat. , 2: 1 , Univ. California Press (1967) pp. 55–61 |
Schauder theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schauder_theorem&oldid=28264