Difference between revisions of "Weak topology"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "A short course of functional analysis" , Moscow (1982) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Springer (1971)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.A. Lyusternik, V.I. Sobolev, "A short course of functional analysis" , Moscow (1982) (In Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H.H. Schaefer, "Topological vector spaces" , Springer (1971) {{MR|0342978}} {{MR|0276721}} {{ZBL|0217.16002}} {{ZBL|0212.14001}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) {{MR|0632257}} {{ZBL|0466.46001}} </TD></TR></table> |
Revision as of 12:13, 27 September 2012
The locally convex topology on a vector space 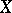 generated by the family of semi-norms (cf. Semi-norm)
generated by the family of semi-norms (cf. Semi-norm) 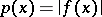 , where
, where 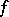 ranges over some subset
ranges over some subset 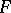 of the (algebraic) adjoint space
of the (algebraic) adjoint space 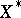 .
.
References
| [1] | L.A. Lyusternik, V.I. Sobolev, "A short course of functional analysis" , Moscow (1982) (In Russian) |
| [2] | H.H. Schaefer, "Topological vector spaces" , Springer (1971) MR0342978 MR0276721 Zbl 0217.16002 Zbl 0212.14001 |
Comments
The weak topology as introduced above is often denoted by 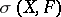 . It is a Hausdorff topology if and only if
. It is a Hausdorff topology if and only if 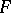 separates the points of
separates the points of 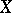 .
.
See also Strong topology.
References
| [a1] | H. Jarchow, "Locally convex spaces" , Teubner (1981) (Translated from German) MR0632257 Zbl 0466.46001 |
How to Cite This Entry:
Weak topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_topology&oldid=17244
Weak topology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weak_topology&oldid=17244
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article