Difference between revisions of "Hausdorff measure"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F. Hausdorff, "Dimension and äusseres Mass" ''Math. Ann.'' , '''79''' (1918) pp. 157–179</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F. Hausdorff, "Dimension and äusseres Mass" ''Math. Ann.'' , '''79''' (1918) pp. 157–179 {{MR|1511917}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958) {{MR|0117523}} {{ZBL|}} </TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Dellacherie, "Ensembles analytiques, capacités, mesures de Hausdorff" , ''Lect. notes in math.'' , '''295''' , Springer (1972)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.-P. Kahane, R. Salem, "Ensembles parfaits et séries trigonométriques" , Hermann (1963) pp. 142</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.-F. le Gall, "Temps locaux d'intersection et points multiples des processus de Lévy" , ''Sem. Probab. XXI'' , ''Lect. notes in math.'' , '''1247''' , Springer (1987) pp. 341–374</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> C.A. Rogers, "Hausdorff measures" , Cambridge Univ. Press (1970)</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) {{MR|0225986}} {{ZBL|0189.10903}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C. Dellacherie, "Ensembles analytiques, capacités, mesures de Hausdorff" , ''Lect. notes in math.'' , '''295''' , Springer (1972) {{MR|0492152}} {{ZBL|0259.31001}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985) {{MR|0867284}} {{ZBL|0587.28004}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 {{MR|0257325}} {{ZBL|0176.00801}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.-P. Kahane, R. Salem, "Ensembles parfaits et séries trigonométriques" , Hermann (1963) pp. 142 {{MR|0160065}} {{ZBL|0112.29304}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> J.-F. le Gall, "Temps locaux d'intersection et points multiples des processus de Lévy" , ''Sem. Probab. XXI'' , ''Lect. notes in math.'' , '''1247''' , Springer (1987) pp. 341–374 {{MR|}} {{ZBL|0621.60077}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111 {{MR|1528565}} {{MR|0053186}} {{ZBL|0050.05603}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> C.A. Rogers, "Hausdorff measures" , Cambridge Univ. Press (1970) {{MR|0281862}} {{ZBL|0204.37601}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) {{MR|1111477}} {{ZBL|0683.32002}} </TD></TR></table> |
Revision as of 12:00, 27 September 2012
A collective name for the class of measures determined on the Borel 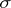 -algebra
-algebra 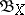 of a metric space
of a metric space 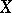 by means of the following construction: Let
by means of the following construction: Let 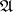 be a certain class of open subsets of
be a certain class of open subsets of 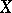 , let
, let 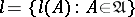 be a non-negative function defined on
be a non-negative function defined on 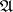 , and let
, and let
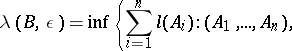 |
 |
where the infimum is taken over all finite or countable coverings of the Borel set  by sets in
by sets in 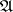 with diameter not exceeding
with diameter not exceeding  . The Hausdorff measure
. The Hausdorff measure 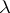 defined by the class
defined by the class 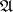 and the function
and the function 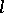 is the limit
is the limit
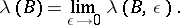 |
Examples of Hausdorff measures. 1) Let 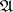 be the collection of all balls in
be the collection of all balls in 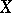 , and let
, and let 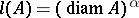 ,
, 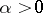 . The corresponding measure
. The corresponding measure 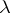 is called the Hausdorff
is called the Hausdorff 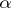 -measure (the linear Hausdorff measure for
-measure (the linear Hausdorff measure for 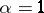 and the plane Hausdorff measure for
and the plane Hausdorff measure for 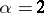 ). 2) Let
). 2) Let 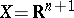 , and let
, and let 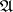 be the collection of cylinders with spherical bases and with axes parallel to the direction of the axis
be the collection of cylinders with spherical bases and with axes parallel to the direction of the axis 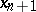 ; let
; let 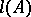 be the
be the  -dimensional volume of the axial section of a cylinder
-dimensional volume of the axial section of a cylinder 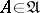 ; the corresponding Hausdorff measure is called the cylindrical measure.
; the corresponding Hausdorff measure is called the cylindrical measure.
The Hausdorff measures were introduced by F. Hausdorff [1].
References
| [1] | F. Hausdorff, "Dimension and äusseres Mass" Math. Ann. , 79 (1918) pp. 157–179 MR1511917 |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
Comments
A method to construct measures on metric spaces was introduced by C. Carathéodory in 1914. The elements of 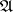 can be anything and are often taken closed. The Hausdorff measures are
can be anything and are often taken closed. The Hausdorff measures are  -additive on the Borel
-additive on the Borel 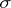 -field, but are in general not
-field, but are in general not 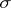 -finite; some restrictions on
-finite; some restrictions on 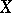 ,
, 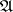 and
and 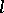 have to be added in order to get nice properties of approximation from below. Such restrictions are, e.g.,
have to be added in order to get nice properties of approximation from below. Such restrictions are, e.g., 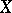 is a Borel subset of some compact metric space,
is a Borel subset of some compact metric space, 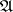 is the class of closed subsets of
is the class of closed subsets of  and
and 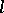 is of the form
is of the form 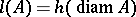 where
where 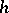 is a continuous non-decreasing function from
is a continuous non-decreasing function from 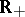 to
to 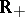 . The measures obtained in this way are the Hausdorff measures most often used, and were mainly studied by A.S. Besicovitch and his school (cf. [a8]); they are called (Hausdorff)
. The measures obtained in this way are the Hausdorff measures most often used, and were mainly studied by A.S. Besicovitch and his school (cf. [a8]); they are called (Hausdorff) 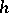 -measures (if
-measures (if 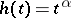 ,
, 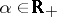 , one says
, one says 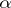 -measure or
-measure or 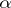 -dimensional measure; see also Hausdorff dimension). When
-dimensional measure; see also Hausdorff dimension). When 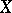 is the Euclidean space
is the Euclidean space 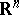 , the
, the 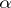 -dimensional measure is equal (up to a multiplicative constant) to the Lebesgue measure if
-dimensional measure is equal (up to a multiplicative constant) to the Lebesgue measure if  and, when restricted to smooth curves, surfaces, etc., is equal to the length, area, etc. if
and, when restricted to smooth curves, surfaces, etc., is equal to the length, area, etc. if 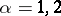 , etc. The
, etc. The  -measure is the counting measure, which is also at the confines of potential theory and descriptive set theory.
-measure is the counting measure, which is also at the confines of potential theory and descriptive set theory.
Even though the notion of Hausdorff measure is not regarded as being fundamental, it appears in many parts of hard analysis and geometry. Through the study of exceptional sets, it is used, for example, in harmonic analysis (cf. [a5]), in potential theory (cf. [a1]), in the metric theory of continued fractions (cf. [a8]), and in differential geometry (cf. Sard theorem). For many reasons it is closely linked to the notion of capacity, and, more generally, to descriptive set theory (cf. [a1], [a2], [a8]; R.O. Davies was, before G. Choquet, the first to prove capacitability theorems). In the theory of stochastic processes it has a crucial role in the fine study of the paths of the Wiener process and others (cf. [a6] and its bibliography). Finally, on 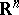 , the
, the 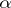 -dimensional measure is, when
-dimensional measure is, when 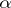 is a natural integer, a fundamental notion in geometric measure theory (cf. Area; Minimal surface, and [a4] in which also Hausdorff measures which are not
is a natural integer, a fundamental notion in geometric measure theory (cf. Area; Minimal surface, and [a4] in which also Hausdorff measures which are not 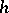 -measures (Favard measure, etc.) are used); for non-integer
-measures (Favard measure, etc.) are used); for non-integer 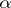 it is a fundamental notion in the theory of fractals (cf. [a3]).
it is a fundamental notion in the theory of fractals (cf. [a3]).
For the use of Hausdorff measures and the Hausdorff dimension in multi-dimensional complex analysis, see, e.g., [a9].
References
| [a1] | L. Carleson, "Selected problems on exceptional sets" , v. Nostrand (1967) MR0225986 Zbl 0189.10903 |
| [a2] | C. Dellacherie, "Ensembles analytiques, capacités, mesures de Hausdorff" , Lect. notes in math. , 295 , Springer (1972) MR0492152 Zbl 0259.31001 |
| [a3] | K.J. Falconer, "The geometry of fractal sets" , Cambridge Univ. Press (1985) MR0867284 Zbl 0587.28004 |
| [a4] | H. Federer, "Geometric measure theory" , Springer (1969) pp. 60; 62; 71; 108 MR0257325 Zbl 0176.00801 |
| [a5] | J.-P. Kahane, R. Salem, "Ensembles parfaits et séries trigonométriques" , Hermann (1963) pp. 142 MR0160065 Zbl 0112.29304 |
| [a6] | J.-F. le Gall, "Temps locaux d'intersection et points multiples des processus de Lévy" , Sem. Probab. XXI , Lect. notes in math. , 1247 , Springer (1987) pp. 341–374 Zbl 0621.60077 |
| [a7] | M.E. Munroe, "Introduction to measure and integration" , Addison-Wesley (1953) pp. 111 MR1528565 MR0053186 Zbl 0050.05603 |
| [a8] | C.A. Rogers, "Hausdorff measures" , Cambridge Univ. Press (1970) MR0281862 Zbl 0204.37601 |
| [a9] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) (Translated from Russian) MR1111477 Zbl 0683.32002 |
Hausdorff measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hausdorff_measure&oldid=18209