Difference between revisions of "Barrier"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) pp. Chapt. 3 (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1985) pp. Chapt. 3 (In Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German) {{MR|0195654}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) pp. Chapt. 3 (Translated from Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Shabat, "Introduction of complex analysis" , '''1–2''' , Moscow (1985) pp. Chapt. 3 (In Russian) {{MR|}} {{ZBL|0578.32001}} {{ZBL|0574.30001}} </TD></TR></table> |
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , '''1''' , Cambridge Univ. Press (1976)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.L. Helms, "Introduction to potential theory" , Acad. Press (1975) (Translated from German)</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , '''1''' , Cambridge Univ. Press (1976) {{MR|0460672}} {{MR|0419791}} {{MR|0412442}} {{MR|0442324}} {{ZBL|0419.31001}} {{ZBL|0339.31003}} {{ZBL|0328.33011}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> L.L. Helms, "Introduction to potential theory" , Acad. Press (1975) (Translated from German) {{MR|0460666}} {{ZBL|0188.17203}} </TD></TR></table> |
Latest revision as of 11:57, 27 September 2012
Lebesgue barrier, in potential theory
A function the existence of which is a necessary and sufficient condition for the regularity of a boundary point with respect to the behaviour of a generalized solution of the Dirichlet problem at that point (cf. Perron method; Regular boundary point).
Let 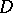 be a domain in a Euclidean space
be a domain in a Euclidean space  ,
,  , and let
, and let 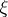 be a point on its boundary
be a point on its boundary 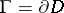 . A barrier for the point
. A barrier for the point  is any function
is any function 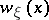 , continuous in the intersection
, continuous in the intersection  of the closed domain
of the closed domain  with some ball
with some ball  with centre at
with centre at 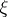 , which is superharmonic in
, which is superharmonic in 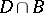 and positive in
and positive in 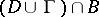 , except at
, except at 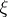 , at which it vanishes. For instance, if
, at which it vanishes. For instance, if 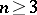 and
and 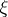 is any boundary point for which there exists a closed ball
is any boundary point for which there exists a closed ball 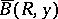 in
in 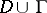 which meets
which meets 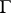 only in
only in 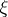 , one can take as a barrier the harmonic function
, one can take as a barrier the harmonic function
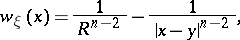 |
where  is the radius of
is the radius of 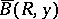 and
and 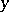 is its centre.
is its centre.
A barrier in the theory of functions of (several) complex variables is a function the existence of which for all boundary points of the domain 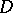 implies that
implies that 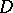 is a domain of holomorphy. Let
is a domain of holomorphy. Let 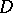 be a domain in the complex space
be a domain in the complex space 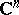 ,
, 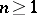 , and let
, and let 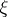 be a point of the boundary
be a point of the boundary 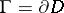 . Any analytic function
. Any analytic function 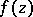 in
in 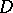 with a singular point at
with a singular point at 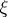 will then be a barrier at
will then be a barrier at 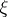 . Thus, the function
. Thus, the function 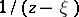 is a barrier for the boundary point
is a barrier for the boundary point  of any plane domain
of any plane domain 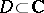 . There also exists a barrier at any point
. There also exists a barrier at any point 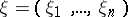 of the boundary of the ball
of the boundary of the ball
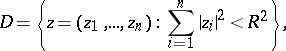 |
e.g. the function  .
.
A barrier exists at a boundary point 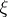 of a domain
of a domain 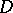 if there is an analytic function defined in
if there is an analytic function defined in 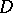 that is unbounded at
that is unbounded at 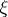 , i.e. is such that for some sequence of points
, i.e. is such that for some sequence of points 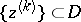 which converges to
which converges to 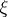 one has:
one has:
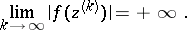 |
The converse is true for domains 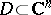 in the following strong form: For any set
in the following strong form: For any set 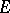 of boundary points of a domain
of boundary points of a domain 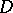 at which a barrier exists, one can find a function holomorphic in
at which a barrier exists, one can find a function holomorphic in 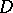 which is unbounded at all points of
which is unbounded at all points of 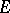 . If
. If 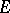 is everywhere dense in the boundary of
is everywhere dense in the boundary of 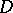 , then
, then 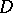 is a domain of holomorphy.
is a domain of holomorphy.
References
| [1] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) MR0195654 |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) pp. Chapt. 3 (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) pp. Chapt. 3 (In Russian) Zbl 0578.32001 Zbl 0574.30001 |
Comments
Good English references for the Lebesgue barrier are [a1] and [a2].
References
| [a1] | W.K. Hayman, P.B. Kennedy, "Subharmonic functions" , 1 , Cambridge Univ. Press (1976) MR0460672 MR0419791 MR0412442 MR0442324 Zbl 0419.31001 Zbl 0339.31003 Zbl 0328.33011 |
| [a2] | L.L. Helms, "Introduction to potential theory" , Acad. Press (1975) (Translated from German) MR0460666 Zbl 0188.17203 |
Barrier. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Barrier&oldid=12033