Approximate derivative

2020 Mathematics Subject Classification: Primary: 28A33 Secondary: 49Q15 [MSN][ZBL]

A generalization of the concept of a derivative, where the ordinary limit is replaced by an approximate limit.

Definition

Consider a (Lebesgure) measurable set $E\subset \mathbb R$, a measurable map $f:E\to \mathbb R^k$ and a point $x_0\in E$ where $E$ has Lebesgue density $1$. If the approximate limit \[ {\rm ap}\, \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} \] exists at it is finite, then it is called approximate derivative of the function $f$ at $x_0$ (some authors include also the case in which the limit is $\pm\infty$). In that case the function $f$ is called approximately differentiable at $x_0$ and, as a consequence of the definition, $f$ is approximately continuous at $x_0$. The concept can be extended further to functions of several variables: see Approximate differentiability Some authors denote the approximate derivative by $f'_{ap} (x_0)$, whereas some authors keep the notation $f' (x_0)$. Indeed if the classical derivative exists, then it coincides with the approximate derivative, whereas the opposite is false (note, for instance, that if $g$ coincides alomst everywhere with $f$, then $g$ is as well approximately differentiable at $x_0$).

Properties

The following useful proposition relates further the two concept.

Proposition 1 Let $E$, $f$ and $x_0$ be as above. The approximate derivative at $x_0$ exists if and only if there is a measurable set $F\subset E$ which has density $1$ at $x_0$ and such that the classical derivative exists for $f|_F$ at $x_0$. Moreover, the approximate derivative at $x_0$ equals the classical derivative of $f_F$ at the same point.

As a corollary of the previous proposition, the classical rules for the differentiation of a sum, a difference, a product, and a quotient of functions apply to (finite) approximate derivatives as well. The theorem on the differentiation of a compositition of approximately differentiable functions does not apply in general. However it applies to $\varphi\circ f$ if $f$ is approximately differentiable at $x_0$ and $\varphi$ is classically differentiable at $f(x_0)$.

Approximate Dini derivatives and Denjoy-Khinchin theorem

Approximate Dini derivatives are defined by analogy with ordinary Dini derivatives (cf. Dini derivative): $D^+ f (x_0)$, $D^- f (x_0)$ and $d^+ f (x_0)$, $d^- f (x_0)$ are, respectively, the right and left approximate upper limits and the right and left approximate lower limits of the quotient \[ \frac{f(x)-f(x_0)}{x-x_0} \] The following theorem applies.

Theorem 2 (Denjoy-Khinchin) If $E\subset \mathbb R$ is (Lebesgue) measurable and $f:E\to mathbb R$ (Lebesgue) measurable, then at almost every point of $x_0\in E$,

• either $f$ has a finite approximate derivative,
• or $D^+ f (x_0)= D^- f (x_0)= \infty$,
• or $d^⁺ f (x_0)= d^- f (x_0)=-\infty$.

Relation with the integral

As it happens for the ordinary derivative, however, the existence almost everywhere of the approximate derivative does not imply that the fundamental theorem of calculus applies, that is: $f$ might be approximately differentiable almost everywhere on the interval $[0,1]$ but nonetheless the identity \[ f (a)-f(b) =\int_a^b f' (t)\, dt \] might fail on a set of positive measure of extrema $(a,b)\in [0,1]^2$ (cp. with the example in Absolute continuity). If

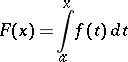is a Denjoy–Khinchin integral, then 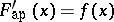almost-everywhere in the interval under consideration (an ordinary derivative need not exist on a set of positive measure). This theorem explains the role played by approximate derivatives in the theory of integrals.

There exist continuous functions without an ordinary or an approximate derivative at any point of a given interval.

Approximate partial derivatives of functions of several real variables are considered as well.

Comments

The concept of an approximate derivative was introduced by >A.Ya. Khinchin in 1916.

References

[1]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)

For other references see Approximate limit.