Difference between revisions of "Approximate derivative"
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| − | + | {{MSC|28A33|49Q15}} | |
| − | + | [[Category:Classical measure theory]] | |
| − | |||
| − | Approximate Dini derivatives are defined by analogy with ordinary Dini derivatives (cf. [[Dini derivative|Dini derivative]]): <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a0128508.png" /> — lim sup from the right; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a0128509.png" /> — lim inf from the right; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285010.png" /> — lim sup from the left; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285011.png" /> — lim inf from the left; for example, | + | {{TEX|done}} |
| + | |||
| + | A generalization of the concept of a derivative, where the ordinary limit is replaced by an [[Approximate limit|approximate limit]]. | ||
| + | |||
| + | ====Definition==== | ||
| + | Consider a (Lebesgure) measurable set $E\subset \mathbb R$, a measurable map $f:E\to \mathbb R^k$ and a point $x_0\in E$ where $E$ has [[Density of a set|Lebesgue density]] $1$. If the approximate limit | ||
| + | \[ | ||
| + | {\rm ap}\, \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} | ||
| + | \] | ||
| + | exists at it is finite, then it is called approximate derivative of the function $f$ at $x_0$ (some authors include also the case in which the limit is $\pm infty$). In that case the function $f$ is called approximately differentiable at $x_0$ and, as a consequence of the definition, $f$ is [[Approximate continuity|approximately continuous]] at $x_0$. The concept can be extended further to functions of several variables: see [[Approximate differentiability]] Some authors denote the approximate derivative by $f'_{ap} (x_0)$, whereas some authors keep the notation $f' (x_0)$. Indeed if the classical derivative exists, then it coincides with the approximate derivative, whereas the opposite is false (note, for instance, that if $g$ coincides alomst everywhere with $f$, then $g$ is as well approximately differentiable at $x_0$). | ||
| + | |||
| + | ====Properties==== | ||
| + | The following useful proposition relates further the two concept. | ||
| + | |||
| + | '''Proposition 1''' | ||
| + | Let $E$, $f$ and $x_0$ be as above. The approximate derivative at $x_0$ exists if and only if there is a measurable set $F\subset E$ which has density $1$ at $x_0$ and such that the classical derivative exists for $f|_F$ at $x_0$. Moreover, the approximate derivative at $x_0$ equals the classical derivative of $f_F$ at the same point. | ||
| + | |||
| + | As a corollary of the previous proposition, the classical rules for the differentiation of a sum, a difference, a product, and a quotient of functions apply to (finite) approximate derivatives as well. The theorem on the differentiation of a compositition of approximately differentiable functions does not apply in general. However it applies to $\varphi\circ f$ if $f$ is approximately differentiable at $x_0$ and $\varphi$ is '''classically differentiable''' at $f(x_0)$. | ||
| + | |||
| + | ====Approximate Dini derivatives and Denjoy-Khinchin theorem==== | ||
| + | Approximate Dini derivatives are defined by analogy with ordinary Dini derivatives (cf. [[Dini derivative|Dini derivative]]): $D^+ (x_0)$, $D^- (x_0)$ | ||
| + | and $d^+ (x_0)$, $d^- (x_0)$ are, respectively, the right and left approximate upper limits and the right and left approximate lower limits of the quotient | ||
| + | \[ | ||
| + | \frac{f(x)-f(x_0)}{x-x_0} | ||
| + | \] | ||
| + | |||
| + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a0128508.png" /> — lim sup from the right; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a0128509.png" /> — lim inf from the right; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285010.png" /> — lim sup from the left; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285011.png" /> — lim inf from the left; for example, | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285012.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012850/a01285012.png" /></td> </tr></table> | ||
| Line 22: | Line 47: | ||
Approximate partial derivatives of functions of several real variables are considered as well. | Approximate partial derivatives of functions of several real variables are considered as well. | ||
| + | |||
| + | ====Comments==== | ||
| + | The concept of an approximate derivative was introduced by >A.Ya. Khinchin in 1916. | ||
| + | |||
====References==== | ====References==== | ||
| Line 28: | Line 57: | ||
| − | + | ||
For other references see [[Approximate limit|Approximate limit]]. | For other references see [[Approximate limit|Approximate limit]]. | ||
Revision as of 06:01, 7 August 2012
2020 Mathematics Subject Classification: Primary: 28A33 Secondary: 49Q15 [MSN][ZBL]
A generalization of the concept of a derivative, where the ordinary limit is replaced by an approximate limit.
Definition
Consider a (Lebesgure) measurable set $E\subset \mathbb R$, a measurable map $f:E\to \mathbb R^k$ and a point $x_0\in E$ where $E$ has Lebesgue density $1$. If the approximate limit \[ {\rm ap}\, \lim_{x\to x_0} \frac{f(x)-f(x_0)}{x-x_0} \] exists at it is finite, then it is called approximate derivative of the function $f$ at $x_0$ (some authors include also the case in which the limit is $\pm infty$). In that case the function $f$ is called approximately differentiable at $x_0$ and, as a consequence of the definition, $f$ is approximately continuous at $x_0$. The concept can be extended further to functions of several variables: see Approximate differentiability Some authors denote the approximate derivative by $f'_{ap} (x_0)$, whereas some authors keep the notation $f' (x_0)$. Indeed if the classical derivative exists, then it coincides with the approximate derivative, whereas the opposite is false (note, for instance, that if $g$ coincides alomst everywhere with $f$, then $g$ is as well approximately differentiable at $x_0$).
Properties
The following useful proposition relates further the two concept.
Proposition 1 Let $E$, $f$ and $x_0$ be as above. The approximate derivative at $x_0$ exists if and only if there is a measurable set $F\subset E$ which has density $1$ at $x_0$ and such that the classical derivative exists for $f|_F$ at $x_0$. Moreover, the approximate derivative at $x_0$ equals the classical derivative of $f_F$ at the same point.
As a corollary of the previous proposition, the classical rules for the differentiation of a sum, a difference, a product, and a quotient of functions apply to (finite) approximate derivatives as well. The theorem on the differentiation of a compositition of approximately differentiable functions does not apply in general. However it applies to $\varphi\circ f$ if $f$ is approximately differentiable at $x_0$ and $\varphi$ is classically differentiable at $f(x_0)$.
Approximate Dini derivatives and Denjoy-Khinchin theorem
Approximate Dini derivatives are defined by analogy with ordinary Dini derivatives (cf. Dini derivative): $D^+ (x_0)$, $D^- (x_0)$ and $d^+ (x_0)$, $d^- (x_0)$ are, respectively, the right and left approximate upper limits and the right and left approximate lower limits of the quotient \[ \frac{f(x)-f(x_0)}{x-x_0} \]
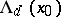 — lim sup from the right;
— lim sup from the right; 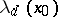 — lim inf from the right;
— lim inf from the right; 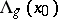 — lim sup from the left;
— lim sup from the left; 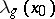 — lim inf from the left; for example,
— lim inf from the left; for example,
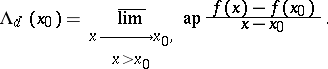 |
The following Denjoy–Khinchin theorems apply. If a real-valued function 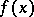 is finite and Lebesgue-measurable on a set
is finite and Lebesgue-measurable on a set 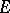 , then, at almost any point of this set, either
, then, at almost any point of this set, either 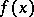 has a finite approximate derivative, or
has a finite approximate derivative, or
 |
If
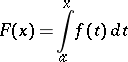 |
is a Denjoy–Khinchin integral, then 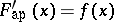 almost-everywhere in the interval under consideration (an ordinary derivative need not exist on a set of positive measure). This theorem explains the role played by approximate derivatives in the theory of integrals.
almost-everywhere in the interval under consideration (an ordinary derivative need not exist on a set of positive measure). This theorem explains the role played by approximate derivatives in the theory of integrals.
There exist continuous functions without an ordinary or an approximate derivative at any point of a given interval.
Approximate partial derivatives of functions of several real variables are considered as well.
Comments
The concept of an approximate derivative was introduced by >A.Ya. Khinchin in 1916.
References
| [1] | S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French) |
For other references see Approximate limit.
Approximate derivative. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximate_derivative&oldid=15032