Difference between revisions of "Measurable function"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|H}}|| P.R. Halmos, "Measure theory" , v. Nostrand (1950) {{MR|0033869}} {{ZBL|0040.16802}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|DS}}|| N. Dunford, J.T. Schwartz, "Linear operators. General theory" , '''1''' , Interscience (1958) {{MR|0117523}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|KF}}|| A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , '''1–2''' , Graylock (1957–1961) (Translated from Russian) {{MR|1025126}} {{MR|0708717}} {{MR|0630899}} {{MR|0435771}} {{MR|0377444}} {{MR|0234241}} {{MR|0215962}} {{MR|0118796}} {{MR|1530727}} {{MR|0118795}} {{MR|0085462}} {{MR|0070045}} {{ZBL|0932.46001}} {{ZBL|0672.46001}} {{ZBL|0501.46001}} {{ZBL|0501.46002}} {{ZBL|0235.46001}} {{ZBL|0103.08801}} | ||
| + | |} | ||
Revision as of 05:54, 15 May 2012
2020 Mathematics Subject Classification: Primary: 28A20 [MSN][ZBL]
Originally, a measurable function was understood to be a function  of a real variable
of a real variable  with the property that for every
with the property that for every  the set
the set  of points
of points  at which
at which  is a (Lebesgue-) measurable set. A measurable function on an interval
is a (Lebesgue-) measurable set. A measurable function on an interval  can be made continuous on
can be made continuous on  by changing its values on a set of arbitrarily small measure; this is the so-called
by changing its values on a set of arbitrarily small measure; this is the so-called 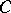 -property of measurable functions (N.N. Luzin, 1913, cf. also Luzin
-property of measurable functions (N.N. Luzin, 1913, cf. also Luzin 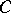 -property).
-property).
A measurable function on a space 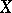 is defined relative to a chosen system
is defined relative to a chosen system 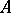 of measurable sets in
of measurable sets in 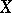 . If
. If 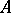 is a
is a 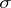 -ring, then a real-valued function
-ring, then a real-valued function 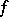 on
on 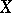 is said to be a measurable function if
is said to be a measurable function if
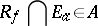 |
for every real number  , where
, where
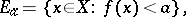 |
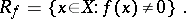 |
This definition is equivalent to the following: A real-valued function  is measurable if
is measurable if
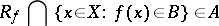 |
for every Borel set  . When
. When 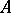 is a
is a 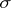 -algebra, a function
-algebra, a function 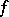 is measurable if
is measurable if 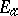 (or
(or 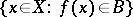 ) is measurable. The class of measurable functions is closed under the arithmetical and lattice operations; that is, if
) is measurable. The class of measurable functions is closed under the arithmetical and lattice operations; that is, if  ,
, 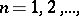 are measurable, then
are measurable, then 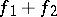 ,
,  ,
, 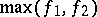 ,
, 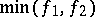 and
and 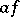 (
( real) are measurable;
real) are measurable; 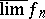 and
and 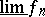 are also measurable. A complex-valued function is measurable if its real and imaginary parts are measurable. A generalization of the concept of a measurable function is that of a measurable mapping from one measurable space to another.
are also measurable. A complex-valued function is measurable if its real and imaginary parts are measurable. A generalization of the concept of a measurable function is that of a measurable mapping from one measurable space to another.
References
| [H] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) MR0033869 Zbl 0040.16802 |
| [DS] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
| [KF] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
Measurable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measurable_function&oldid=23633