Difference between revisions of "Markov property"
(→References: Feller: internal link) |
(refs format) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|GS}}|| I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , '''2''' , Springer (1975) (Translated from Russian) {{MR|0375463}} {{ZBL|0305.60027}} | |
| − | + | |} | |
====Comments==== | ====Comments==== | ||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|C}}|| K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960) {{MR|0116388}} {{ZBL|0092.34304}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|Do}}|| J.L. Doob, "Stochastic processes" , Wiley (1953) {{MR|1570654}} {{MR|0058896}} {{ZBL|0053.26802}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Dy}}|| E.B. Dynkin, "Markov processes" , '''1''' , Springer (1965) (Translated from Russian) {{MR|0193671}} {{ZBL|0132.37901}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| T.G. Kurtz, "Markov processes" , Wiley (1986) {{MR|0838085}} {{ZBL|0592.60049}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F}}|| W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''1–2''' , Wiley (1966) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Le}}|| P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) {{MR|0190953}} {{ZBL|0137.11602}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Lo}}|| M. Loève, "Probability theory" , '''II''' , Springer (1978) {{MR|0651017}} {{MR|0651018}} {{ZBL|0385.60001}} | ||
| + | |} | ||
Revision as of 19:18, 14 May 2012
for a real-valued stochastic process 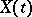 ,
, 
2020 Mathematics Subject Classification: Primary: 60Jxx [MSN][ZBL]
The property that for any set 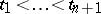 of times from
of times from  and any Borel set
and any Borel set 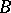 ,
,
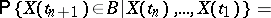 | (*) |
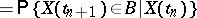 |
with probability 1, that is, the conditional probability distribution of 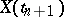 given
given 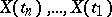 coincides (almost certainly) with the conditional distribution of
coincides (almost certainly) with the conditional distribution of 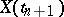 given
given 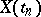 . This can be interpreted as independence of the "future"
. This can be interpreted as independence of the "future" 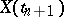 and the "past"
and the "past" 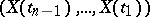 given the fixed "present"
given the fixed "present"  . Stochastic processes satisfying the property (*) are called Markov processes (cf. Markov process). The Markov property has (under certain additional assumptions) a stronger version, known as the "strong Markov property" . In discrete time
. Stochastic processes satisfying the property (*) are called Markov processes (cf. Markov process). The Markov property has (under certain additional assumptions) a stronger version, known as the "strong Markov property" . In discrete time 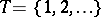 the strong Markov property, which is always true for (Markov) sequences satisfying (*), means that for each stopping time
the strong Markov property, which is always true for (Markov) sequences satisfying (*), means that for each stopping time  (relative to the family of
(relative to the family of 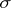 -algebras
-algebras 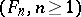 ,
, 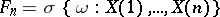 ), with probability one
), with probability one
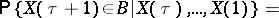 |
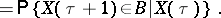 |
References
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) MR0375463 Zbl 0305.60027 |
Comments
References
| [C] | K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960) MR0116388 Zbl 0092.34304 |
| [Do] | J.L. Doob, "Stochastic processes" , Wiley (1953) MR1570654 MR0058896 Zbl 0053.26802 |
| [Dy] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian) MR0193671 Zbl 0132.37901 |
| [K] | T.G. Kurtz, "Markov processes" , Wiley (1986) MR0838085 Zbl 0592.60049 |
| [F] | W. Feller, "An introduction to probability theory and its applications", 1–2 , Wiley (1966) |
| [Le] | P. Lévy, "Processus stochastiques et mouvement Brownien" , Gauthier-Villars (1965) MR0190953 Zbl 0137.11602 |
| [Lo] | M. Loève, "Probability theory" , II , Springer (1978) MR0651017 MR0651018 Zbl 0385.60001 |
Markov property. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_property&oldid=25529