Namespaces
Variants
Actions

Difference between revisions of "Markov chain, decomposable"

From Encyclopedia of Mathematics
Jump to: navigation, search
(→‎References: Feller: internal link)
(refs format)
Line 11: Line 11:
  
 
====References====
 
====References====
−
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its  applications"|"An introduction to probability theory and its  applications"]], '''1–2''', Wiley (1966) </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D. Freedman, "Markov chains", Holden-Day (1975) {{MR|0686269}} {{MR|0681291}} {{MR|0556418}} {{MR|0428472}} {{MR|0292176}} {{MR|0237001}} {{MR|0211464}} {{MR|0164375}} {{MR|0158435}} {{MR|0152015}} {{ZBL|0501.60071}} {{ZBL|0501.60069}} {{ZBL|0426.60064}} {{ZBL|0325.60059}} {{ZBL|0322.60057}} {{ZBL|0212.49801}} {{ZBL|0129.30605}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Iosifescu, "Finite Markov processes and their applications", Wiley (1980) {{MR|0587116}} {{ZBL|0436.60001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> J.G. Kemeny, J.L. Snell, "Finite Markov chains", v. Nostrand (1960) {{MR|1531032}} {{MR|0115196}} {{ZBL|0089.13704}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains", Springer (1976) {{MR|0407981}} {{ZBL|0348.60090}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> D. Revuz, "Markov chains", North-Holland (1975) {{MR|0415773}} {{ZBL|0332.60045}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> V.I. [V.I. Romanovskii] Romanovsky, "Discrete Markov chains", Wolters-Noordhoff (1970) (Translated from Russian) {{MR|0266312}} {{ZBL|0201.20002}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> E. Seneta, "Non-negative matrices and Markov chains", Springer (1981) {{MR|2209438}} {{ZBL|0471.60001}} </TD></TR></table>
+
{|
 +
|valign="top"|{{Ref|F}}|| W. Feller, [[Feller, "An introduction to probability theory and its  applications"|"An introduction to probability theory and its  applications"]], '''1–2''', Wiley (1966)
 +
|-
 +
|valign="top"|{{Ref|Fr}}|| D. Freedman, "Markov chains", Holden-Day (1975) {{MR|0686269}} {{MR|0681291}} {{MR|0556418}} {{MR|0428472}} {{MR|0292176}} {{MR|0237001}} {{MR|0211464}} {{MR|0164375}} {{MR|0158435}} {{MR|0152015}} {{ZBL|0501.60071}} {{ZBL|0501.60069}} {{ZBL|0426.60064}} {{ZBL|0325.60059}} {{ZBL|0322.60057}} {{ZBL|0212.49801}} {{ZBL|0129.30605}}
 +
|-
 +
|valign="top"|{{Ref|I}}|| M. Iosifescu, "Finite Markov processes and their applications", Wiley (1980) {{MR|0587116}} {{ZBL|0436.60001}}
 +
|-
 +
|valign="top"|{{Ref|KS}}|| J.G. Kemeny, J.L. Snell, "Finite Markov chains", v. Nostrand (1960) {{MR|1531032}} {{MR|0115196}} {{ZBL|0089.13704}}
 +
|-
 +
|valign="top"|{{Ref|KSK}}|| J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains", Springer (1976) {{MR|0407981}} {{ZBL|0348.60090}}
 +
|-
 +
|valign="top"|{{Ref|Re}}|| D. Revuz, "Markov chains", North-Holland (1975) {{MR|0415773}} {{ZBL|0332.60045}}
 +
|-
 +
|valign="top"|{{Ref|Ro}}|| V.I. Romanovsky, "Discrete Markov chains", Wolters-Noordhoff (1970) (Translated from Russian) {{MR|0266312}} {{ZBL|0201.20002}}
 +
|-
 +
|valign="top"|{{Ref|S}}|| E. Seneta, "Non-negative matrices and Markov chains", Springer (1981) {{MR|2209438}} {{ZBL|0471.60001}}
 +
|}

Revision as of 06:23, 14 May 2012

2020 Mathematics Subject Classification: Primary: 60J10 Secondary: 60J27 [MSN][ZBL]

A Markov chain whose transition probabilities 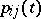have the following property: There are states 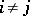such that 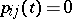for all 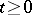. Decomposability of a Markov chain is equivalent to decomposability of its matrix of transition probabilities 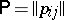for discrete-time Markov chains, and of its matrix of transition probability densities 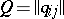, , 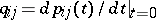for continuous-time Markov chains. The state space of a decomposable Markov chain consists either of inessential states or of more than one class of communicating states (cf. Markov chain).


Comments

References

[F] W. Feller, "An introduction to probability theory and its applications", 1–2, Wiley (1966)
[Fr] D. Freedman, "Markov chains", Holden-Day (1975) MR0686269 MR0681291 MR0556418 MR0428472 MR0292176 MR0237001 MR0211464 MR0164375 MR0158435 MR0152015 Zbl 0501.60071 Zbl 0501.60069 Zbl 0426.60064 Zbl 0325.60059 Zbl 0322.60057 Zbl 0212.49801 Zbl 0129.30605
[I] M. Iosifescu, "Finite Markov processes and their applications", Wiley (1980) MR0587116 Zbl 0436.60001
[KS] J.G. Kemeny, J.L. Snell, "Finite Markov chains", v. Nostrand (1960) MR1531032 MR0115196 Zbl 0089.13704
[KSK] J.G. Kemeny, J.L. Snell, A.W. Knapp, "Denumerable Markov chains", Springer (1976) MR0407981 Zbl 0348.60090
[Re] D. Revuz, "Markov chains", North-Holland (1975) MR0415773 Zbl 0332.60045
[Ro] V.I. Romanovsky, "Discrete Markov chains", Wolters-Noordhoff (1970) (Translated from Russian) MR0266312 Zbl 0201.20002
[S] E. Seneta, "Non-negative matrices and Markov chains", Springer (1981) MR2209438 Zbl 0471.60001
How to Cite This Entry:
Markov chain, decomposable. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_chain,_decomposable&oldid=25966
This article was adapted from an original article by B.A. Sevast'yanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Markov_chain,_decomposable&oldid=26565"