Difference between revisions of "Feller process"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 7: | Line 7: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838014.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838014.png" /></td> </tr></table> | ||
| − | is continuous. This requirement on the transition function is natural because the transition operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838016.png" />, acting on the space of bounded Borel functions, leave invariant the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838017.png" /> of continuous bounded functions, that is, the semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838018.png" /> of transition operators can be considered as acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838019.png" />. The first semi-groups of this type were studied by W. Feller (1952, see | + | is continuous. This requirement on the transition function is natural because the transition operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838016.png" />, acting on the space of bounded Borel functions, leave invariant the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838017.png" /> of continuous bounded functions, that is, the semi-group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838018.png" /> of transition operators can be considered as acting on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838019.png" />. The first semi-groups of this type were studied by W. Feller (1952, see {{Cite|D}}). |
| − | As a rule, one imposes additional conditions on the topological space; usually <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838020.png" /> is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see [[Markov process|Markov process]], the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838021.png" />; a basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838022.png" /> is constituted by the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838023.png" /> such that the first exit moment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838024.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838025.png" /> almost-surely satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838026.png" /> if the process starts in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838027.png" /> (see | + | As a rule, one imposes additional conditions on the topological space; usually <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838020.png" /> is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see [[Markov process|Markov process]], the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838021.png" />; a basis of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838022.png" /> is constituted by the sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838023.png" /> such that the first exit moment <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838024.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838025.png" /> almost-surely satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838026.png" /> if the process starts in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838027.png" /> (see {{Cite|D}}). |
| − | An important subclass of Feller processes is formed by the strong Feller processes | + | An important subclass of Feller processes is formed by the strong Feller processes {{Cite|G}}; in this case a stricter smoothness condition is imposed on the transition function: The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838028.png" /> must be continuous for every bounded Borel function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838029.png" />. If, moreover, the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838030.png" /> is continuous in the variation norm in the space of bounded measures, then the Markov process corresponding to this transition function is called a strong Feller process in the narrow sense. If the transition functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838032.png" /> correspond to strong Feller processes, then their composition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838033.png" /> corresponds to a strong Feller process in the narrow sense under the usual assumptions on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838034.png" />. Non-degenerate diffusion processes (cf. [[Diffusion process|Diffusion process]]) are strong Feller processes (see {{Cite|M}}). A natural generalization of strong Feller processes are Markov processes with a continuous component (see {{Cite|TT}}). |
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838035.png" /> is a subset of the natural numbers, then a Feller process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838036.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838037.png" />, is called a Feller chain. An example of a Feller chain is provided by a [[Random walk|random walk]] on the line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838038.png" />: a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838040.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838041.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838042.png" /> is a sequence of independent identically-distributed random variables. Here the random walk <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838043.png" /> is a strong Feller chain if and only if the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838044.png" /> has a density. | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838035.png" /> is a subset of the natural numbers, then a Feller process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838036.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838037.png" />, is called a Feller chain. An example of a Feller chain is provided by a [[Random walk|random walk]] on the line <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838038.png" />: a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838039.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838040.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838041.png" />, and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838042.png" /> is a sequence of independent identically-distributed random variables. Here the random walk <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838043.png" /> is a strong Feller chain if and only if the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838044.png" /> has a density. | ||
| − | There is a natural generalization for Feller processes of the classification of the states of a Markov chain with a countable number of states (see [[Markov chain|Markov chain]]). Two states <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838046.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838047.png" /> are in communication if for any neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838048.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838050.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838051.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838052.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838053.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838054.png" /> (chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical [[Ergodic theory|ergodic theory]]. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see | + | There is a natural generalization for Feller processes of the classification of the states of a Markov chain with a countable number of states (see [[Markov chain|Markov chain]]). Two states <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838045.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838046.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838047.png" /> are in communication if for any neighbourhoods <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838048.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838049.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838050.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838051.png" /> there are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838052.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838053.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838054.png" /> (chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical [[Ergodic theory|ergodic theory]]. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see {{Cite|Sm}}). Here the ergodic properties of a Feller process are of a comparatively weak nature. |
| − | As an example one can compare properties such as recurrence for a Markov chain with a general space of states. Suppose that for any initial state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838055.png" /> and any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838056.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838057.png" /> it is almost-surely true that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838058.png" /> for an infinite set of values of the time <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838059.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838060.png" /> takes values in the natural numbers). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838061.png" /> is a system of sets of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838062.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838063.png" /> is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see | + | As an example one can compare properties such as recurrence for a Markov chain with a general space of states. Suppose that for any initial state <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838055.png" /> and any set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838056.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838057.png" /> it is almost-surely true that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838058.png" /> for an infinite set of values of the time <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838059.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838060.png" /> takes values in the natural numbers). If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838061.png" /> is a system of sets of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838062.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838063.png" /> is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see {{Cite|R}}), and if for the Feller process one chooses as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838064.png" /> the topology <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838065.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838066.png" />, the diffusion (topological recurrence) property is obtained (see {{Cite|Sm}}). A random walk <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838067.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838068.png" /> has finite expectation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838069.png" /> is a diffusion Feller chain if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838070.png" />, and if the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838071.png" /> is not arithmetic, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838072.png" /> is moreover recurrent in the sense of Harris only if for some <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838073.png" /> the distribution of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838074.png" /> has an absolutely-continuous component. |
| − | From the formal point of view, the theory of Markov chains with a general state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838075.png" /> can be reduced to the study of Feller chains with a compact state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838076.png" /> — the extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838077.png" /> obtained by means of the Gel'fand–Naimark theorem (see [[Banach algebra|Banach algebra]] and | + | From the formal point of view, the theory of Markov chains with a general state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838075.png" /> can be reduced to the study of Feller chains with a compact state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838076.png" /> — the extension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838077.png" /> obtained by means of the Gel'fand–Naimark theorem (see [[Banach algebra|Banach algebra]] and {{Cite|Z}}). This extension, however, is "too large" ; other constructions of Feller extensions are also possible for Markov chains (see {{Cite|Sh}}). |
The theory of Feller processes and Feller chains is also a probabilistic generalization of [[Topological dynamics|topological dynamics]], since a deterministic (degenerate) Feller process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838078.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838079.png" />, corresponds to the dynamical system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838080.png" />, where the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838081.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838082.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838083.png" /> is continuous and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838084.png" /> (almost-surely). | The theory of Feller processes and Feller chains is also a probabilistic generalization of [[Topological dynamics|topological dynamics]], since a deterministic (degenerate) Feller process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838078.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838079.png" />, corresponds to the dynamical system <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838080.png" />, where the mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838081.png" /> from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838082.png" /> into <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838083.png" /> is continuous and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f038/f038380/f03838084.png" /> (almost-surely). | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|D}}|| E.B. Dynkin, "Markov processes" , '''1–2''' , Springer (1965) (Translated from Russian) {{MR|0193671}} {{ZBL|0132.37901}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|G}}|| I.V. Girsanov, "On transforming a certain class of stochastic processes by absolutely continuous substitution of measures" ''Theor. Probab. Appl.'' , '''5''' : 3 (1960) pp. 285–301 ''Teor. Veroyatnost. i Primenen.'' , '''5''' : 3 (1960) pp. 314–330 {{MR|133152}} {{ZBL|0100.34004}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|M}}|| S.A. Molchanov, "Strong Feller property of diffusion processes on smooth manifolds" ''Theor. Probab. Appl.'' , '''13''' : 3 (1968) pp. 471–475 ''Teor. Veroyatnost. i Primenen.'' , '''13''' : 3 (1968) pp. 493–498 {{MR|}} {{ZBL|0177.21805}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|TT}}|| P. Tuominen, R. Tweedie, "Markov chains with continuous components" ''Proc. London Math. Soc.'' , '''38''' (1979) pp. 89–114 {{MR|0520974}} {{ZBL|0396.60059}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Fo}}|| S. Foguel, "The ergodic theory of positive operators on continuous functions" ''Ann. Scuola Norm. Sup. Pisa'' , '''27''' : 1 (1973) pp. 19–51 {{MR|0372154}} {{ZBL|0258.47010}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Si}}|| R. Sine, "Sample path convergence of stable Markov processes II" ''Indiana Univ. Math. J.'' , '''25''' : 1 (1976) pp. 23–43 {{MR|0391261}} {{ZBL|0329.60021}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Sm}}|| S.N. Smirnov, "On the asymptotic behavior of Feller chains" ''Soviet Math. Dokl.'' , '''25''' : 2 (1982) pp. 399–403 ''Dokl. Akad. Nauk SSSR'' , '''263''' : 3 (1982) pp. 554–558 {{MR|0650363}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|R}}|| D. Revuz, "Markov chains" , North-Holland (1975) {{MR|0415773}} {{ZBL|0332.60045}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Z}}|| A.I. Zhdanok, "Ergodic theorems for nonsmooth Markov processes" , ''Topological spaces and their mappings'' , Riga (1981) pp. 18–33 (In Russian) (English summary) {{MR|0630418}} {{ZBL|0477.60061}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Sh}}|| M.G. Shur, "Invariant measures for Markov chains and Feller extensions of chains" ''Theory Probab. Appl.'' , '''26''' : 3 (1981) pp. 485–497 ''Teor. Veroyatnost. i Primenen.'' , '''26''' : 3 (1981) pp. 496–509 {{MR|0627857}} {{ZBL|0499.60074}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 38: | Line 56: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|DM}}|| C. Dellacherie, P.A. Meyer, "Probabilities and potential" , '''C''' , North-Holland (1988) (Translated from French) {{MR|0939365}} {{ZBL|0716.60001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F}}|| W. Feller, "An introduction to probability theory and its applications" , '''2''' , Wiley (1966) pp. Chapt. X {{MR|0210154}} {{ZBL|0138.10207}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|L}}|| M. Loève, "Probability theory" , Princeton Univ. Press (1963) pp. Chapt. XIV {{MR|0203748}} {{ZBL|0108.14202}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|C}}|| K.L. Chung, "Lectures from Markov processes to Brownian motion" , Springer (1982) {{MR|0648601}} {{ZBL|0503.60073}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|W}}|| A.D. [A.D. Ventsel'] Wentzell, "A course in the theory of stochastic processes" , McGraw-Hill (1981) (Translated from Russian) {{MR|0781738}} {{MR|0614594}} {{ZBL|0502.60001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|K}}|| T.G. Kurtz, "Markov processes" , Wiley (1986) {{MR|0838085}} {{ZBL|0592.60049}} | ||
| + | |} | ||
Revision as of 06:23, 13 May 2012
2020 Mathematics Subject Classification: Primary: 60J35 [MSN][ZBL]
A homogeneous Markov process  ,
,  , where
, where  is an additive sub-semi-group of the real axis
is an additive sub-semi-group of the real axis  , with values in a topological space
, with values in a topological space 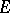 with a topology
with a topology  and a Borel
and a Borel  -algebra
-algebra  , the transition function
, the transition function  ,
, 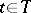 ,
, 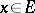 ,
,  , of which has a certain property of smoothness, namely that for a continuous bounded function
, of which has a certain property of smoothness, namely that for a continuous bounded function  the function
the function
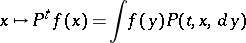 |
is continuous. This requirement on the transition function is natural because the transition operators 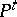 ,
,  , acting on the space of bounded Borel functions, leave invariant the space
, acting on the space of bounded Borel functions, leave invariant the space 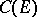 of continuous bounded functions, that is, the semi-group
of continuous bounded functions, that is, the semi-group  of transition operators can be considered as acting on
of transition operators can be considered as acting on 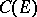 . The first semi-groups of this type were studied by W. Feller (1952, see [D]).
. The first semi-groups of this type were studied by W. Feller (1952, see [D]).
As a rule, one imposes additional conditions on the topological space; usually  is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see Markov process, the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology
is a locally compact metrizable space. In this case, a Feller process that satisfies the condition of stochastic continuity admits a modification that is a standard Markov process (see Markov process, the strong Markov property). Conversely, a standard Markov process is a Feller process for a natural topology 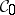 ; a basis of
; a basis of 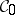 is constituted by the sets
is constituted by the sets 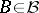 such that the first exit moment
such that the first exit moment  from
from 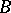 almost-surely satisfies
almost-surely satisfies 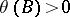 if the process starts in
if the process starts in 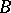 (see [D]).
(see [D]).
An important subclass of Feller processes is formed by the strong Feller processes [G]; in this case a stricter smoothness condition is imposed on the transition function: The function 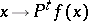 must be continuous for every bounded Borel function
must be continuous for every bounded Borel function  . If, moreover, the function
. If, moreover, the function 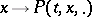 is continuous in the variation norm in the space of bounded measures, then the Markov process corresponding to this transition function is called a strong Feller process in the narrow sense. If the transition functions
is continuous in the variation norm in the space of bounded measures, then the Markov process corresponding to this transition function is called a strong Feller process in the narrow sense. If the transition functions 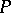 and
and 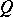 correspond to strong Feller processes, then their composition
correspond to strong Feller processes, then their composition 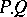 corresponds to a strong Feller process in the narrow sense under the usual assumptions on
corresponds to a strong Feller process in the narrow sense under the usual assumptions on 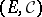 . Non-degenerate diffusion processes (cf. Diffusion process) are strong Feller processes (see [M]). A natural generalization of strong Feller processes are Markov processes with a continuous component (see [TT]).
. Non-degenerate diffusion processes (cf. Diffusion process) are strong Feller processes (see [M]). A natural generalization of strong Feller processes are Markov processes with a continuous component (see [TT]).
If 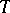 is a subset of the natural numbers, then a Feller process
is a subset of the natural numbers, then a Feller process 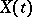 ,
, 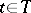 , is called a Feller chain. An example of a Feller chain is provided by a random walk on the line
, is called a Feller chain. An example of a Feller chain is provided by a random walk on the line 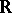 : a sequence
: a sequence  ,
, 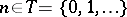 , where
, where 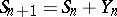 , and
, and 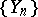 is a sequence of independent identically-distributed random variables. Here the random walk
is a sequence of independent identically-distributed random variables. Here the random walk 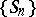 is a strong Feller chain if and only if the distribution of
is a strong Feller chain if and only if the distribution of 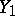 has a density.
has a density.
There is a natural generalization for Feller processes of the classification of the states of a Markov chain with a countable number of states (see Markov chain). Two states  and
and  in
in  are in communication if for any neighbourhoods
are in communication if for any neighbourhoods 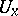 of
of  and
and 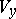 of
of 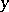 there are
there are 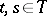 such that
such that 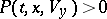 and
and  (chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical ergodic theory. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see [Sm]). Here the ergodic properties of a Feller process are of a comparatively weak nature.
(chains with a countable set of states are Feller chains with the discrete topology). Ergodic properties and methods for investigating them have a definite character for Feller processes in comparison to classical ergodic theory. The "most-regular" behaviour is found with irreducible (topologically-indecomposable) Feller processes; these are Feller processes all states of which are in communication (see [Sm]). Here the ergodic properties of a Feller process are of a comparatively weak nature.
As an example one can compare properties such as recurrence for a Markov chain with a general space of states. Suppose that for any initial state 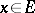 and any set
and any set  in
in 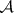 it is almost-surely true that
it is almost-surely true that 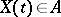 for an infinite set of values of the time
for an infinite set of values of the time 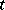 (
(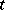 takes values in the natural numbers). If
takes values in the natural numbers). If  is a system of sets of the form
is a system of sets of the form 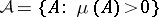 , where
, where 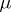 is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see [R]), and if for the Feller process one chooses as
is some measure, then one obtains the recurrence property of a chain in the sense of Harris (see [R]), and if for the Feller process one chooses as  the topology
the topology  on
on 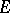 , the diffusion (topological recurrence) property is obtained (see [Sm]). A random walk
, the diffusion (topological recurrence) property is obtained (see [Sm]). A random walk 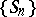 for which
for which 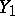 has finite expectation
has finite expectation 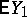 is a diffusion Feller chain if and only if
is a diffusion Feller chain if and only if 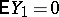 , and if the distribution of
, and if the distribution of  is not arithmetic, then
is not arithmetic, then 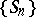 is moreover recurrent in the sense of Harris only if for some
is moreover recurrent in the sense of Harris only if for some  the distribution of
the distribution of 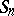 has an absolutely-continuous component.
has an absolutely-continuous component.
From the formal point of view, the theory of Markov chains with a general state space 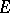 can be reduced to the study of Feller chains with a compact state space
can be reduced to the study of Feller chains with a compact state space  — the extension of
— the extension of 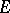 obtained by means of the Gel'fand–Naimark theorem (see Banach algebra and [Z]). This extension, however, is "too large" ; other constructions of Feller extensions are also possible for Markov chains (see [Sh]).
obtained by means of the Gel'fand–Naimark theorem (see Banach algebra and [Z]). This extension, however, is "too large" ; other constructions of Feller extensions are also possible for Markov chains (see [Sh]).
The theory of Feller processes and Feller chains is also a probabilistic generalization of topological dynamics, since a deterministic (degenerate) Feller process  ,
,  , corresponds to the dynamical system
, corresponds to the dynamical system  , where the mapping
, where the mapping 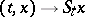 from
from  into
into 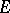 is continuous and
is continuous and 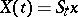 (almost-surely).
(almost-surely).
References
| [D] | E.B. Dynkin, "Markov processes" , 1–2 , Springer (1965) (Translated from Russian) MR0193671 Zbl 0132.37901 |
| [G] | I.V. Girsanov, "On transforming a certain class of stochastic processes by absolutely continuous substitution of measures" Theor. Probab. Appl. , 5 : 3 (1960) pp. 285–301 Teor. Veroyatnost. i Primenen. , 5 : 3 (1960) pp. 314–330 MR133152 Zbl 0100.34004 |
| [M] | S.A. Molchanov, "Strong Feller property of diffusion processes on smooth manifolds" Theor. Probab. Appl. , 13 : 3 (1968) pp. 471–475 Teor. Veroyatnost. i Primenen. , 13 : 3 (1968) pp. 493–498 Zbl 0177.21805 |
| [TT] | P. Tuominen, R. Tweedie, "Markov chains with continuous components" Proc. London Math. Soc. , 38 (1979) pp. 89–114 MR0520974 Zbl 0396.60059 |
| [Fo] | S. Foguel, "The ergodic theory of positive operators on continuous functions" Ann. Scuola Norm. Sup. Pisa , 27 : 1 (1973) pp. 19–51 MR0372154 Zbl 0258.47010 |
| [Si] | R. Sine, "Sample path convergence of stable Markov processes II" Indiana Univ. Math. J. , 25 : 1 (1976) pp. 23–43 MR0391261 Zbl 0329.60021 |
| [Sm] | S.N. Smirnov, "On the asymptotic behavior of Feller chains" Soviet Math. Dokl. , 25 : 2 (1982) pp. 399–403 Dokl. Akad. Nauk SSSR , 263 : 3 (1982) pp. 554–558 MR0650363 |
| [R] | D. Revuz, "Markov chains" , North-Holland (1975) MR0415773 Zbl 0332.60045 |
| [Z] | A.I. Zhdanok, "Ergodic theorems for nonsmooth Markov processes" , Topological spaces and their mappings , Riga (1981) pp. 18–33 (In Russian) (English summary) MR0630418 Zbl 0477.60061 |
| [Sh] | M.G. Shur, "Invariant measures for Markov chains and Feller extensions of chains" Theory Probab. Appl. , 26 : 3 (1981) pp. 485–497 Teor. Veroyatnost. i Primenen. , 26 : 3 (1981) pp. 496–509 MR0627857 Zbl 0499.60074 |
Comments
In the West a Feller process is usually indexed by 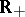 (and not by
(and not by 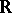 ). Feller processes are important for three main reasons:
). Feller processes are important for three main reasons:
a) numerous natural (homogeneous) Markov processes are Feller; e.g., a diffusion process, a stochastic process with stationary increments, among them a Wiener process and a Poisson process;
b) the notion of a Feller semi-group (i.e. a transition-operator semi-group 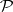 as defined in the main article) lies at the interface between the stochastic and the analytic study of semi-groups of linear operators (see also Semi-group of operators);
as defined in the main article) lies at the interface between the stochastic and the analytic study of semi-groups of linear operators (see also Semi-group of operators);
c) by way of the so-called Ray–Knight compactification it is possible to look at a strong Markov process as if it were "almost" a Feller process (with a nice topology on the state space), and so the make use of the smoothness of the latter.
References
| [DM] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French) MR0939365 Zbl 0716.60001 |
| [F] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) pp. Chapt. X MR0210154 Zbl 0138.10207 |
| [L] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) pp. Chapt. XIV MR0203748 Zbl 0108.14202 |
| [C] | K.L. Chung, "Lectures from Markov processes to Brownian motion" , Springer (1982) MR0648601 Zbl 0503.60073 |
| [W] | A.D. [A.D. Ventsel'] Wentzell, "A course in the theory of stochastic processes" , McGraw-Hill (1981) (Translated from Russian) MR0781738 MR0614594 Zbl 0502.60001 |
| [K] | T.G. Kurtz, "Markov processes" , Wiley (1986) MR0838085 Zbl 0592.60049 |
Feller process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Feller_process&oldid=23608