Fatou ring

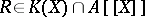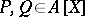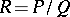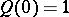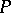An integral domain $A$ with quotient field $K$ such that if each rational function $R\in K(X)$ that has a Taylor expansion at $0$ with coefficients in $A$, has a unitary and irreducible representation with coefficients in $A$; that is, for each there are such that , and and 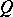are relatively prime in . Fatou's lemma [a1] states that 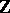is a Fatou ring.

Equivalently, 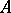is a Fatou ring means that if a sequence 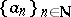of elements of 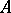satisfies a linear recursion formula

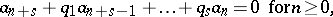where 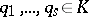and is as small as possible, then .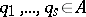

If 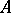is a Fatou ring, then its quotient field 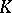is a Fatou extension of 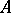, but the converse does not hold. This is the reason why Fatou rings are sometimes called strong Fatou rings, while the domains 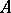such that 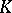is a Fatou extension of 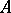are called weak Fatou rings (in this latter case, every 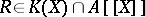has a unitary (not necessarily irreducible) representation with coefficients in ).

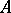The coefficients of the unitary and irreducible representation of every element of 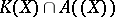are almost integral over 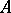(see Fatou extension). An integral domain 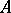is a Fatou ring if and only if every element of 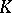which is almost integral over 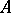belongs to 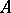[a2]; such domains are said to be completely integrally closed. For instance, a Noetherian domain (cf. also Noetherian ring) is completely integrally closed if and only if it is integrally closed (cf. also Integral domain). The rings of integers of number fields are completely integrally closed, and hence, Fatou rings.

The notion may be extended by considering formal power series in non-commuting variables. The characterization of this generalized property is still (1998) an open question.

References

[a1]	P. Fatou, "Sur les séries entières à coefficients entiers" C.R. Acad. Sci. Paris Ser. A , 138 (1904) pp. 342–344
[a2]	S. Eilenberg, "Automata, languages and machines" , A , Acad. Press (1974)