Fatou ring
An integral domain 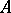 with quotient field
with quotient field 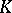 such that if each rational function
such that if each rational function 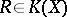 that has a Taylor expansion at
that has a Taylor expansion at  with coefficients in
with coefficients in 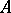 , has a unitary and irreducible representation with coefficients in
, has a unitary and irreducible representation with coefficients in 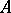 ; that is, for each
; that is, for each 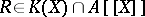 there are
there are 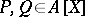 such that
such that 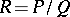 ,
, 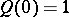 and
and 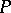 and
and 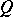 are relatively prime in
are relatively prime in  . Fatou's lemma [a1] states that
. Fatou's lemma [a1] states that 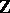 is a Fatou ring.
is a Fatou ring.
Equivalently, 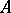 is a Fatou ring means that if a sequence
is a Fatou ring means that if a sequence 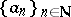 of elements of
of elements of 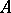 satisfies a linear recursion formula
satisfies a linear recursion formula
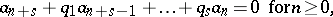 |
where 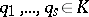 and
and  is as small as possible, then
is as small as possible, then 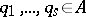 .
.
If 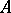 is a Fatou ring, then its quotient field
is a Fatou ring, then its quotient field 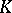 is a Fatou extension of
is a Fatou extension of 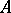 , but the converse does not hold. This is the reason why Fatou rings are sometimes called strong Fatou rings, while the domains
, but the converse does not hold. This is the reason why Fatou rings are sometimes called strong Fatou rings, while the domains 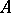 such that
such that 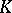 is a Fatou extension of
is a Fatou extension of 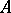 are called weak Fatou rings (in this latter case, every
are called weak Fatou rings (in this latter case, every 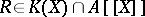 has a unitary (not necessarily irreducible) representation with coefficients in
has a unitary (not necessarily irreducible) representation with coefficients in 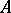 ).
).
The coefficients of the unitary and irreducible representation of every element of 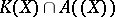 are almost integral over
are almost integral over 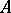 (see Fatou extension). An integral domain
(see Fatou extension). An integral domain 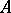 is a Fatou ring if and only if every element of
is a Fatou ring if and only if every element of 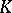 which is almost integral over
which is almost integral over 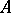 belongs to
belongs to 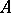 [a2]; such domains are said to be completely integrally closed. For instance, a Noetherian domain (cf. also Noetherian ring) is completely integrally closed if and only if it is integrally closed (cf. also Integral domain). The rings of integers of number fields are completely integrally closed, and hence, Fatou rings.
[a2]; such domains are said to be completely integrally closed. For instance, a Noetherian domain (cf. also Noetherian ring) is completely integrally closed if and only if it is integrally closed (cf. also Integral domain). The rings of integers of number fields are completely integrally closed, and hence, Fatou rings.
The notion may be extended by considering formal power series in non-commuting variables. The characterization of this generalized property is still (1998) an open question.
References
| [a1] | P. Fatou, "Sur les séries entières à coefficients entiers" C.R. Acad. Sci. Paris Ser. A , 138 (1904) pp. 342–344 |
| [a2] | S. Eilenberg, "Automata, languages and machines" , A , Acad. Press (1974) |
Fatou ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fatou_ring&oldid=14976