Difference between revisions of "Contact surgery"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Barden, "Simply connected five-manifolds" ''Ann. of Math.'' , '''82''' (1965) pp. 365–385 {{MR|0184241}} {{ZBL|0136.20602}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> Y. Eliashberg, "Topological characterization of Stein manifolds of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020065.png" />" ''Internat. J. Math.'' , '''1''' (1990) pp. 29–46 {{MR|1044658}} {{ZBL|0699.58002}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H. Geiges, "Applications of contact surgery" ''Topology'' , '''36''' (1997) pp. 1193–1220 {{MR|1452848}} {{ZBL|0912.57019}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> H. Geiges, "Constructions of contact manifolds" ''Math. Proc. Cambridge Philos. Soc.'' , '''121''' (1997) pp. 455–464 {{MR|1434654}} {{ZBL|0882.57007}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R.E. Gompf, "Handlebody construction of Stein surfaces" ''Ann. of Math.'' , '''148''' (1998) pp. 619–693 {{MR|1668563}} {{ZBL|0919.57012}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> M. Gromov, H.B. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" ''Ann. of Math.'' , '''111''' (1980) pp. 423–434 {{MR|0577131}} {{ZBL|0463.53025}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> J. Martinet, "Formes de contact sur les variétés de dimension<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020066.png" />" , ''Proc. Liverpool Singularities Sympos. II'' , ''Lecture Notes Math.'' , '''209''' , Springer (1971) pp. 142–163 {{MR|0350771}} {{ZBL|0215.23003}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> J. Milnor, "Morse theory" , Princeton Univ. Press (1963) {{MR|0163331}} {{ZBL|0108.10401}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> R. Schoen, S.T. Yau, "On the structure of manifolds with positive scalar curvature" ''Manuscripta Math.'' , '''28''' (1979) pp. 159–183 {{MR|0535700}} {{ZBL|0423.53032}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> J.-P. Sha, D.-G. Yang, "Positive Ricci curvature on the connected sum of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c120/c120200/c12020067.png" />" ''J. Diff. Geom.'' , '''33''' (1991) pp. 127–137 {{MR|1085137}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A. Weinstein, "Contact surgery and symplectic handlebodies" ''Hokkaido Math. J.'' , '''20''' (1991) pp. 241–251 {{MR|1114405}} {{ZBL|0737.57012}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> D. Wraith, "Surgery on Ricci positive manifolds" ''J. Reine Angew. Math.'' , '''501''' (1998) pp. 99–113 {{MR|1637825}} {{ZBL|0915.53018}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
A special type of surgery on a (strict) contact manifold 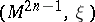 (i.e. a smooth manifold admitting a (strict) contact structure
(i.e. a smooth manifold admitting a (strict) contact structure  , where
, where 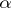 is a
is a 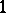 -form satisfying
-form satisfying 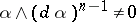 ), which results in a new contact manifold.
), which results in a new contact manifold.
In topological terms, surgery on 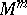 denotes the replacement of an embedded copy of
denotes the replacement of an embedded copy of 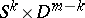 , a tubular neighbourhood of an embedded
, a tubular neighbourhood of an embedded 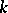 -sphere with trivial normal bundle, by a copy of
-sphere with trivial normal bundle, by a copy of 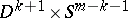 , with the obvious identification along the boundary
, with the obvious identification along the boundary 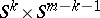 . Alternatively, one can attach a
. Alternatively, one can attach a 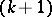 -handle
-handle 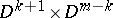 along
along 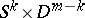 to a manifold
to a manifold 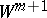 with boundary
with boundary 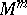 , and the new boundary will be the result of performing surgery on
, and the new boundary will be the result of performing surgery on 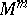 .
.
As shown by Y. Eliashberg [a2] and A. Weinstein [a11], contact surgery is possible along spheres which are isotropic submanifolds (cf. also Isotropic submanifold) of 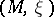 and have trivial normal bundle. The choice of framing, i.e. trivialization of the normal bundle, for which contact surgery is possible is restricted.
and have trivial normal bundle. The choice of framing, i.e. trivialization of the normal bundle, for which contact surgery is possible is restricted.
A contact manifold 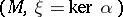 may be regarded as the strictly pseudo-convex boundary of an almost-complex (in fact, symplectic) manifold
may be regarded as the strictly pseudo-convex boundary of an almost-complex (in fact, symplectic) manifold 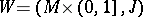 such that
such that 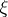 is given by the
is given by the 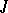 -invariant subspace of the tangent bundle
-invariant subspace of the tangent bundle 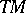 . Contact surgery on
. Contact surgery on 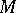 can then be interpreted as the attaching of an almost-complex or symplectic handle to
can then be interpreted as the attaching of an almost-complex or symplectic handle to  along
along 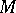 , and the framing condition for
, and the framing condition for 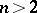 is given by requiring the almost-complex structure on
is given by requiring the almost-complex structure on 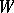 to extend over the handle. For
to extend over the handle. For 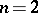 the situation is more subtle, see [a2], [a5]. Weinstein formulates his construction in terms of symplectic handle-bodies, Eliashberg (whose results are somewhat stronger) in terms of
the situation is more subtle, see [a2], [a5]. Weinstein formulates his construction in terms of symplectic handle-bodies, Eliashberg (whose results are somewhat stronger) in terms of 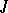 -convex Morse functions on almost-complex manifolds (cf. also Almost-complex structure; Morse function).
-convex Morse functions on almost-complex manifolds (cf. also Almost-complex structure; Morse function).
A Stein manifold of real dimension 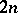 has the homotopy type of an
has the homotopy type of an  -dimensional CW-complex, cf. [a8], p. 39. Eliashberg uses his construction to show that for
-dimensional CW-complex, cf. [a8], p. 39. Eliashberg uses his construction to show that for 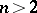 this is indeed the only topological restriction on a Stein manifold, that is, if
this is indeed the only topological restriction on a Stein manifold, that is, if 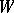 is a
is a 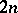 -dimensional smooth manifold with an almost-complex structure
-dimensional smooth manifold with an almost-complex structure 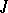 and a proper Morse function
and a proper Morse function 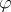 with critical points of Morse index at most
with critical points of Morse index at most  , then
, then 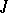 is homotopic to a genuine complex structure
is homotopic to a genuine complex structure 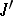 such that
such that 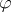 is
is 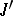 -convex and, in particular,
-convex and, in particular, 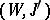 is Stein.
is Stein.
The usefulness of contact surgery in this and other applications rests on the fact that there is an 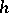 -principle for isotropic spheres. This allows one to replace a given embedding
-principle for isotropic spheres. This allows one to replace a given embedding 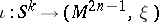 by an isotropic embedding
by an isotropic embedding 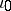 (for
(for 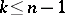 ) that is isotopic to the initial one, provided only an obvious necessary bundle condition is satisfied: If
) that is isotopic to the initial one, provided only an obvious necessary bundle condition is satisfied: If 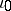 is an isotropic embedding, then its differential
is an isotropic embedding, then its differential 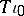 extends to a complex bundle monomorphism
extends to a complex bundle monomorphism 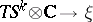 , where
, where 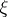 inherits a complex structure from the (conformal) symplectic structure
inherits a complex structure from the (conformal) symplectic structure 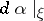 . The relevant
. The relevant 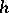 -principle says that, conversely, the existence of such a bundle mapping covering
-principle says that, conversely, the existence of such a bundle mapping covering  is sufficient for
is sufficient for  to be isotopic to an isotropic embedding
to be isotopic to an isotropic embedding 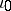 .
.
This allows one to use topological structure theorems, such as Barden's classification of simply-connected  -manifolds [a1], to construct contact structures on a wide class of higher-dimensional manifolds, see [a3].
-manifolds [a1], to construct contact structures on a wide class of higher-dimensional manifolds, see [a3].
In dimension  (
(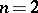 ) there is a different notion of contact surgery, due to R. Lutz and J. Martinet [a7]; it allows surgery along
) there is a different notion of contact surgery, due to R. Lutz and J. Martinet [a7]; it allows surgery along  -spheres embedded transversely to a contact structure
-spheres embedded transversely to a contact structure 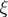 . This was used by Lutz and Martinet to show the existence of a contact structure on any closed, orientable
. This was used by Lutz and Martinet to show the existence of a contact structure on any closed, orientable  -manifold and in any homotopy class of
-manifold and in any homotopy class of  -plane fields. For applications of other topological structure theorems (such as branched coverings or open book decompositions, cf. also Open book decomposition) to the construction of contact manifolds, see [a4] and references therein.
-plane fields. For applications of other topological structure theorems (such as branched coverings or open book decompositions, cf. also Open book decomposition) to the construction of contact manifolds, see [a4] and references therein.
Other types of surgery compatible with some geometric structure include surgery on manifolds of positive scalar curvature ([a6], [a9]) and surgery on manifolds of positive Ricci curvature ([a10], [a12]).
References
| [a1] | D. Barden, "Simply connected five-manifolds" Ann. of Math. , 82 (1965) pp. 365–385 MR0184241 Zbl 0136.20602 |
| [a2] | Y. Eliashberg, "Topological characterization of Stein manifolds of dimension 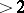 " Internat. J. Math. , 1 (1990) pp. 29–46 MR1044658 Zbl 0699.58002 " Internat. J. Math. , 1 (1990) pp. 29–46 MR1044658 Zbl 0699.58002 |
| [a3] | H. Geiges, "Applications of contact surgery" Topology , 36 (1997) pp. 1193–1220 MR1452848 Zbl 0912.57019 |
| [a4] | H. Geiges, "Constructions of contact manifolds" Math. Proc. Cambridge Philos. Soc. , 121 (1997) pp. 455–464 MR1434654 Zbl 0882.57007 |
| [a5] | R.E. Gompf, "Handlebody construction of Stein surfaces" Ann. of Math. , 148 (1998) pp. 619–693 MR1668563 Zbl 0919.57012 |
| [a6] | M. Gromov, H.B. Lawson Jr., "The classification of simply connected manifolds of positive scalar curvature" Ann. of Math. , 111 (1980) pp. 423–434 MR0577131 Zbl 0463.53025 |
| [a7] | J. Martinet, "Formes de contact sur les variétés de dimension " , Proc. Liverpool Singularities Sympos. II , Lecture Notes Math. , 209 , Springer (1971) pp. 142–163 MR0350771 Zbl 0215.23003 " , Proc. Liverpool Singularities Sympos. II , Lecture Notes Math. , 209 , Springer (1971) pp. 142–163 MR0350771 Zbl 0215.23003 |
| [a8] | J. Milnor, "Morse theory" , Princeton Univ. Press (1963) MR0163331 Zbl 0108.10401 |
| [a9] | R. Schoen, S.T. Yau, "On the structure of manifolds with positive scalar curvature" Manuscripta Math. , 28 (1979) pp. 159–183 MR0535700 Zbl 0423.53032 |
| [a10] | J.-P. Sha, D.-G. Yang, "Positive Ricci curvature on the connected sum of 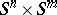 " J. Diff. Geom. , 33 (1991) pp. 127–137 MR1085137 " J. Diff. Geom. , 33 (1991) pp. 127–137 MR1085137 |
| [a11] | A. Weinstein, "Contact surgery and symplectic handlebodies" Hokkaido Math. J. , 20 (1991) pp. 241–251 MR1114405 Zbl 0737.57012 |
| [a12] | D. Wraith, "Surgery on Ricci positive manifolds" J. Reine Angew. Math. , 501 (1998) pp. 99–113 MR1637825 Zbl 0915.53018 |
Contact surgery. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Contact_surgery&oldid=16386