Difference between revisions of "Linear representation, invariant of a"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) {{MR|0000255}} {{ZBL|1024.20502}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) {{MR|0473097}} {{MR|0473098}} {{ZBL|0228.22013}} </TD></TR></table> |
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> T.A. Springer, "Invariant theory" , ''Lect. notes in math.'' , '''585''' , Springer (1977) {{MR|0447428}} {{ZBL|0346.20020}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 {{MR|0323842}} {{ZBL|0254.17004}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) {{MR|0781344}} {{ZBL|0581.22009}} </TD></TR></table> |
Revision as of 10:54, 1 April 2012
A vector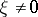 
in the space 
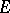of a representation 
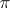of a group 
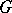(cf. Representation of a group) such that 
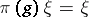for all 
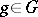. An invariant of a linear representation 
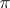of a Lie algebra 
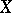is a vector 
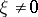in the space 
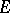of 
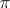such that 
for all 
. In particular, if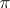 
is a representation of a linear group in a space of multilinear functions, the given definition of the invariant of a linear representation coincides with the classical definition. The invariants of a linear representation arising from restricting an irreducible representation to a subgroup play an important role in the representation theory of Lie groups and Lie algebras (cf. Representation of a Lie algebra).
References
| [1] | H. Weyl, "The classical groups, their invariants and representations" , Princeton Univ. Press (1946) MR0000255 Zbl 1024.20502 |
| [2] | D.P. Zhelobenko, "Compact Lie groups and their representations" , Amer. Math. Soc. (1973) (Translated from Russian) MR0473097 MR0473098 Zbl 0228.22013 |
Comments
References
| [a1] | T.A. Springer, "Invariant theory" , Lect. notes in math. , 585 , Springer (1977) MR0447428 Zbl 0346.20020 |
| [a2] | J.E. Humphreys, "Introduction to Lie algebras and representation theory" , Springer (1972) pp. §5.4 MR0323842 Zbl 0254.17004 |
| [a3] | Th. Bröcker, T. Tom Dieck, "Representations of compact Lie groups" , Springer (1985) MR0781344 Zbl 0581.22009 |
How to Cite This Entry:
Linear representation, invariant of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation,_invariant_of_a&oldid=12505
Linear representation, invariant of a. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_representation,_invariant_of_a&oldid=12505
This article was adapted from an original article by A.I. Shtern (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article