Difference between revisions of "Witt algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G.B. Seligman, "Modular Lie algebras" , Springer (1967) {{MR|0245627}} {{ZBL|0189.03201}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N. Jacobson, "Classes of restricted Lie algebras of characteristic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w098/w098060/w09806068.png" />, II" ''Duke Math. J.'' , '''10''' (1943) pp. 107–121</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R. Ree, "On generalised Witt algebras" ''Trans. Amer. Math. Soc.'' , '''83''' (1956) pp. 510–546</TD></TR></table> |
Revision as of 17:35, 31 March 2012
Let  be a field of characteristic
be a field of characteristic  . Consider the
. Consider the  -algebra
-algebra
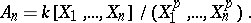 |
Let  be the algebra of
be the algebra of  -derivations of
-derivations of  . The algebra
. The algebra  is known as the Witt algebra. The
is known as the Witt algebra. The  (
(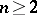 ) are known as the split Jacobson–Witt algebras. The algebra
) are known as the split Jacobson–Witt algebras. The algebra 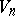 is a simple Lie algebra, except when it is
is a simple Lie algebra, except when it is  -dimensional. The dimension of
-dimensional. The dimension of 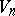 is
is  .
.
More generally one considers the  -algebras
-algebras
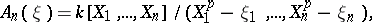 |
and their algebras of derivations  , the Jacobson–Witt algebras. The
, the Jacobson–Witt algebras. The  and
and  are (obviously)
are (obviously)  -forms of
-forms of  and
and 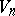 , where
, where 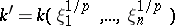 (cf. Form of an (algebraic) structure). Many simple Lie algebras in characteristic
(cf. Form of an (algebraic) structure). Many simple Lie algebras in characteristic  arise as subalgebras of the
arise as subalgebras of the  .
.
Let  be an additive group of functions on
be an additive group of functions on  into
into  such that the only element
such that the only element  of
of  such that
such that 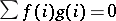 for all
for all  is the zero element
is the zero element  . For instance,
. For instance,  can be the set of all functions from
can be the set of all functions from  to some additive subgroup of
to some additive subgroup of  . If
. If  is finite, it is of order
is finite, it is of order  for some
for some  . Now, let
. Now, let  be a vector space over
be a vector space over  with basis elements
with basis elements 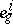 ,
,  ,
,  , and define a bilinear product on
, and define a bilinear product on 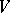 by
by
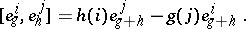 |
There results a Lie algebra, called a generalized Witt algebra. If 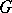 is finite of order
is finite of order  , the dimension of
, the dimension of  is
is  , and
, and  is a simple Lie algebra if
is a simple Lie algebra if  or
or  .
.
If 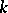 is of characteristic zero,
is of characteristic zero,  and
and  is the additive subgroup
is the additive subgroup 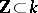 , the same construction results in the Virasoro algebra
, the same construction results in the Virasoro algebra  .
.
If  is of characteristic
is of characteristic  and
and  is the group of all functions on
is the group of all functions on 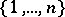 with values in
with values in  , one recovers the Jacobson–Witt algebras
, one recovers the Jacobson–Witt algebras  .
.
There are no isomorphisms between the Jacobson–Witt algebras  and the classical Lie algebras in positive characteristic when
and the classical Lie algebras in positive characteristic when  . Several more classes of simple Lie algebras different from the classical ones and the
. Several more classes of simple Lie algebras different from the classical ones and the  are known, [a1].
are known, [a1].
The Witt algebra(s) described here should of course not be confused with the Witt ring of quadratic forms over a field, nor with the various rings of Witt vectors, cf. Witt vector.
References
| [a1] | G.B. Seligman, "Modular Lie algebras" , Springer (1967) MR0245627 Zbl 0189.03201 |
| [a2] | N. Jacobson, "Classes of restricted Lie algebras of characteristic 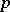 , II" Duke Math. J. , 10 (1943) pp. 107–121 , II" Duke Math. J. , 10 (1943) pp. 107–121 |
| [a3] | R. Ree, "On generalised Witt algebras" Trans. Amer. Math. Soc. , 83 (1956) pp. 510–546 |
Witt algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Witt_algebra&oldid=17520