Difference between revisions of "Weierstrass point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 {{MR|0092855}} {{ZBL|0078.06602}} </TD></TR></table> |
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , '''1''' , Springer (1985) {{MR|0770932}} {{ZBL|0559.14017}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> R.C. Gunning, "Lectures on Riemann surfaces" , Princeton Univ. Press (1966) {{MR|0207977}} {{ZBL|0175.36801}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A point on an algebraic curve (or on a Riemann surface) 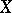 of genus
of genus 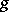 at which the following condition is satisfied: There exists a non-constant rational function on
at which the following condition is satisfied: There exists a non-constant rational function on 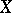 which has at this point a pole of order not exceeding
which has at this point a pole of order not exceeding 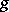 and which has no singularities at other points of
and which has no singularities at other points of 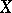 . Only a finite number of Weierstrass points can exist on
. Only a finite number of Weierstrass points can exist on 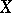 , and if
, and if 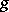 is 0 or 1, there are no such points at all, while if
is 0 or 1, there are no such points at all, while if 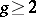 , Weierstrass points must exist. These results were obtained for Riemann surfaces by K. Weierstrass. For algebraic curves of genus
, Weierstrass points must exist. These results were obtained for Riemann surfaces by K. Weierstrass. For algebraic curves of genus 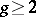 there always exist at least
there always exist at least 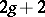 Weierstrass points, and only hyper-elliptic curves of genus
Weierstrass points, and only hyper-elliptic curves of genus 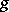 have exactly
have exactly 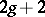 Weierstrass points. The upper bound on the number of Weierstrass points is
Weierstrass points. The upper bound on the number of Weierstrass points is 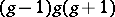 . The presence of a Weierstrass point on an algebraic curve
. The presence of a Weierstrass point on an algebraic curve 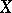 of genus
of genus 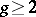 ensures the existence of a morphism of degree not exceeding
ensures the existence of a morphism of degree not exceeding  from the curve
from the curve 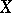 onto the projective line
onto the projective line 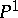 .
.
References
| [1] | N.G. Chebotarev, "The theory of algebraic functions" , Moscow-Leningrad (1948) (In Russian) |
| [2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 MR0092855 Zbl 0078.06602 |
Comments
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a2] | E. Arbarello, M. Cornalba, P.A. Griffiths, J.E. Harris, "Geometry of algebraic curves" , 1 , Springer (1985) MR0770932 Zbl 0559.14017 |
| [a3] | R.C. Gunning, "Lectures on Riemann surfaces" , Princeton Univ. Press (1966) MR0207977 Zbl 0175.36801 |
Weierstrass point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_point&oldid=12917