Difference between revisions of "Unicursal curve"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====Comments==== | ====Comments==== | ||
| − | In algebraic geometry, a unicursal curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517013.png" /> is a rational curve, i.e. a curve that admits a parametric representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517015.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517017.png" /> rational functions. Such a curve is an algebraic curve of effective genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517018.png" />. For every irreducible curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517019.png" /> there exists a birationally equivalent non-singular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517020.png" />. This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517021.png" /> is unique up to isomorphism. The genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517022.png" /> is called the effective genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517023.png" />. The unicursal curves are the irreducible algebraic curves of effective genus zero. This (more or less) agrees with the general geometric definition above, in that the parametrization provides a | + | In algebraic geometry, a unicursal curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517013.png" /> is a rational curve, i.e. a curve that admits a parametric representation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517015.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517016.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517017.png" /> rational functions. Such a curve is an algebraic curve of effective genus <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517018.png" />. For every irreducible curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517019.png" /> there exists a birationally equivalent non-singular curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517020.png" />. This <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517021.png" /> is unique up to isomorphism. The genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517022.png" /> is called the effective genus of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/u/u095/u095170/u09517023.png" />. The unicursal curves are the irreducible algebraic curves of effective genus zero. This (more or less) agrees with the general geometric definition above, in that the parametrization provides a "traversion" . |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R.J. Walker, "Algebraic curves" , Dover, reprint (1950) pp. 149–151 {{MR|0033083}} {{ZBL|0039.37701}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743 {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A plane curve 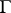 which may be traversed such that the points of self-intersection are visited only twice. For a curve to be unicursal it is necessary and sufficient that there are at most two points through which there pass an odd number of paths. If
which may be traversed such that the points of self-intersection are visited only twice. For a curve to be unicursal it is necessary and sufficient that there are at most two points through which there pass an odd number of paths. If 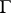 is a plane algebraic curve of order
is a plane algebraic curve of order  having the maximum number
having the maximum number 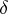 of double points (including improper and imaginary ones), then
of double points (including improper and imaginary ones), then 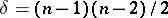 (where a point of multiplicity
(where a point of multiplicity 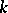 is counted as
is counted as 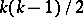 double points).
double points).
Every integral 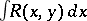 , where
, where 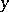 is the function of
is the function of  defined by the equation
defined by the equation  giving an algebraic unicursal curve and
giving an algebraic unicursal curve and 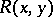 is a rational function, can be reduced to an integral of a rational function and can be expressed in terms of elementary functions.
is a rational function, can be reduced to an integral of a rational function and can be expressed in terms of elementary functions.
Comments
In algebraic geometry, a unicursal curve 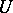 is a rational curve, i.e. a curve that admits a parametric representation
is a rational curve, i.e. a curve that admits a parametric representation 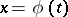 ,
, 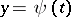 with
with 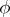 and
and 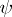 rational functions. Such a curve is an algebraic curve of effective genus
rational functions. Such a curve is an algebraic curve of effective genus  . For every irreducible curve
. For every irreducible curve 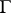 there exists a birationally equivalent non-singular curve
there exists a birationally equivalent non-singular curve 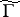 . This
. This  is unique up to isomorphism. The genus of
is unique up to isomorphism. The genus of 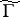 is called the effective genus of
is called the effective genus of 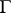 . The unicursal curves are the irreducible algebraic curves of effective genus zero. This (more or less) agrees with the general geometric definition above, in that the parametrization provides a "traversion" .
. The unicursal curves are the irreducible algebraic curves of effective genus zero. This (more or less) agrees with the general geometric definition above, in that the parametrization provides a "traversion" .
References
| [a1] | R.J. Walker, "Algebraic curves" , Dover, reprint (1950) pp. 149–151 MR0033083 Zbl 0039.37701 |
| [a2] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743 MR0507725 Zbl 0408.14001 |
Unicursal curve. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unicursal_curve&oldid=12032