Difference between revisions of "Multiple point"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 9: | Line 9: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) {{MR|0120551}} {{ZBL|0085.36403}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) pp. 173 (Translated from German) {{MR|0046650}} {{ZBL|0047.38806}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Fulton, "Algebraic curves" , Benjamin (1969) pp. 66 {{MR|0313252}} {{MR|0260752}} {{ZBL|0194.21901}} {{ZBL|0181.23901}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
of a planar curve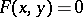 
A singular point at which the partial derivatives of order up to and including 
vanish, but where at least one partial derivative of order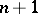 
does not vanish. For example, if 
, 
, 
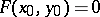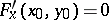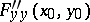does not vanish, the multiple point 
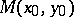is called a double point; if the first and second partial derivatives vanish at 
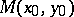, but at least one third derivative does not, the multiple point is called a triple point; etc.
Comments
References
| [a1] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) MR0120551 Zbl 0085.36403 |
| [a2] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) pp. 173 (Translated from German) MR0046650 Zbl 0047.38806 |
| [a3] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a4] | W. Fulton, "Algebraic curves" , Benjamin (1969) pp. 66 MR0313252 MR0260752 Zbl 0194.21901 Zbl 0181.23901 |
How to Cite This Entry:
Multiple point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiple_point&oldid=15154
Multiple point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiple_point&oldid=15154
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article