Difference between revisions of "Intersection index (in algebraic geometry)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 17: | Line 17: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Chapt. IV (Translated from Russian) {{MR|0366917}} {{ZBL|0284.14001}} </TD></TR></table> |
Revision as of 21:53, 30 March 2012
The number of points in the intersection of  divisors (cf. Divisor) in an
divisors (cf. Divisor) in an  -dimensional algebraic variety with allowance for the multiplicities of these points. More precisely, let
-dimensional algebraic variety with allowance for the multiplicities of these points. More precisely, let 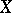 be an
be an  -dimensional non-singular algebraic variety over a field
-dimensional non-singular algebraic variety over a field 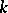 , and let
, and let 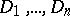 be effective divisors in
be effective divisors in 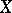 that intersect in a finite number of points. The local index (or multiplicity) of intersection of these divisors at a point
that intersect in a finite number of points. The local index (or multiplicity) of intersection of these divisors at a point 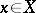 is the integer
is the integer
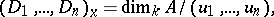 |
where 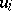 is the local equation for the divisor
is the local equation for the divisor 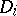 in the local ring
in the local ring 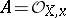 . In the complex case, the local index coincides with the residue of the form
. In the complex case, the local index coincides with the residue of the form 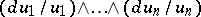 , and also with the degree of the germ of the mapping (cf. Degree of a mapping)
, and also with the degree of the germ of the mapping (cf. Degree of a mapping)
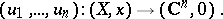 |
The global intersection index 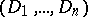 is the sum of the local indices over all points of the intersection
is the sum of the local indices over all points of the intersection  . If this intersection is not empty, then
. If this intersection is not empty, then 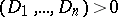 .
.
See also Intersection theory.
Comments
References
| [a1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1974) pp. Chapt. IV (Translated from Russian) MR0366917 Zbl 0284.14001 |
Intersection index (in algebraic geometry). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Intersection_index_(in_algebraic_geometry)&oldid=18849